Symmetric Tree in Java (Time Complexity: O(n))

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

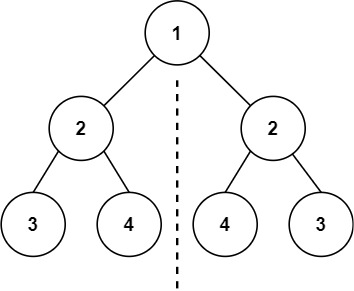
Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

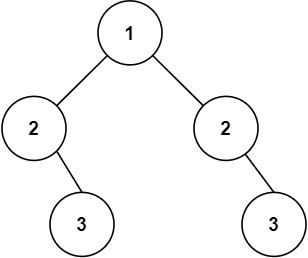
Input: root = [1,2,2,null,3,null,3]
Output: false

Constraints:

The number of nodes in the tree is in the range [1, 1000].
-100 <= Node.val <= 100

Follow up: Could you solve it both recursively and iteratively?

Understanding the Problem

The core challenge of this problem is to determine if a binary tree is symmetric around its center. This means that the left subtree should be a mirror reflection of the right subtree.

Common applications of this problem include validating data structures that need to be symmetric, such as certain types of balanced trees.

Potential pitfalls include not correctly handling null nodes or assuming that the tree is always balanced.

Approach

To solve this problem, we can use two main approaches: recursive and iterative.

Recursive Approach

The recursive approach involves checking if the left subtree is a mirror reflection of the right subtree. This can be done by writing a helper function that compares two nodes and their respective subtrees.

Iterative Approach

The iterative approach uses a queue to perform a level-order traversal, comparing nodes at each level to ensure they are mirror images of each other.

Algorithm

Recursive Algorithm

Define a helper function that takes two nodes as parameters.
Check if both nodes are null. If so, return true.
If only one of the nodes is null, return false.
Check if the values of the two nodes are equal.
Recursively check the left subtree of the first node with the right subtree of the second node and the right subtree of the first node with the left subtree of the second node.

Iterative Algorithm

Use a queue to store pairs of nodes to be compared.
Initialize the queue with the left and right children of the root.
While the queue is not empty, dequeue a pair of nodes and compare them.
If both nodes are null, continue to the next pair.
If only one of the nodes is null or their values are not equal, return false.
Enqueue the left and right children of both nodes in the appropriate order for comparison.

Code Implementation

Recursive Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        return isMirror(root.left, root.right);
    }

    private boolean isMirror(TreeNode t1, TreeNode t2) {
        if (t1 == null && t2 == null) return true;
        if (t1 == null || t2 == null) return false;
        return (t1.val == t2.val)
            && isMirror(t1.right, t2.left)
            && isMirror(t1.left, t2.right);
    }
}

Iterative Solution

import java.util.LinkedList;
import java.util.Queue;

public class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root.left);
        queue.add(root.right);
        while (!queue.isEmpty()) {
            TreeNode t1 = queue.poll();
            TreeNode t2 = queue.poll();
            if (t1 == null && t2 == null) continue;
            if (t1 == null || t2 == null) return false;
            if (t1.val != t2.val) return false;
            queue.add(t1.left);
            queue.add(t2.right);
            queue.add(t1.right);
            queue.add(t2.left);
        }
        return true;
    }
}

Complexity Analysis

Both the recursive and iterative solutions have a time complexity of O(n), where n is the number of nodes in the tree. This is because each node is visited once.

The space complexity for the recursive solution is O(h), where h is the height of the tree, due to the call stack. For the iterative solution, the space complexity is O(n) due to the queue.

Edge Cases

Potential edge cases include:

An empty tree (should return true).
A tree with only one node (should return true).
Subtrees that are not balanced but still symmetric.

Testing

To test the solution comprehensively, consider the following test cases:

An empty tree.
A tree with a single node.
A symmetric tree with multiple levels.
A non-symmetric tree with multiple levels.

Thinking and Problem-Solving Tips

When approaching such problems, it is helpful to:

Break down the problem into smaller subproblems.
Consider both recursive and iterative solutions.
Draw diagrams to visualize the problem.
Write pseudocode before implementing the actual code.

Conclusion

Understanding and solving the symmetric tree problem is crucial for mastering tree-based algorithms. It helps in developing a deeper understanding of tree traversal techniques and recursive problem-solving.

Practice is key to mastering these concepts. Try solving similar problems and explore different tree traversal algorithms to improve your skills.

Additional Resources

For further reading and practice, consider the following resources: