N Queens Problem in Java with Time Complexity Analysis

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, and is represented as an array containing the column for each row of the matrix.

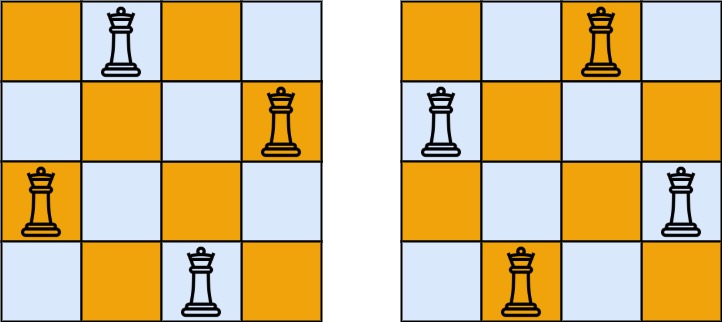
Example:

Input: n = 4
Output: [[1, 3, 0, 2], [2, 0, 3, 1]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Constraints:

1 <= n <= 9

Understanding the Problem

The core challenge of the n-queens problem is to place n queens on an n x n chessboard such that no two queens can attack each other. This means no two queens can be in the same row, column, or diagonal.

This problem is significant in the field of computer science and mathematics, particularly in the study of algorithms and combinatorial optimization. It has applications in various fields such as parallel computing, constraint satisfaction problems, and artificial intelligence.

Potential pitfalls include misunderstanding the constraints of the problem, such as ensuring that no two queens share the same diagonal, which can be tricky to implement correctly.

Approach

To solve the n-queens problem, we can use a backtracking approach. Backtracking is a general algorithm for finding all (or some) solutions to computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot possibly be completed to a valid solution.

Naive Solution

A naive solution would involve generating all possible configurations of queens on the board and then checking each configuration to see if it meets the constraints. This approach is not optimal due to its high time complexity.

Optimized Solution

The optimized solution involves using backtracking to place queens one by one in different columns, starting from the leftmost column. When placing a queen in a column, we check for clashes with already placed queens. If a clash is found, we backtrack and try the next column. If no clash is found, we move to the next row and repeat the process.

Algorithm

Here is a step-by-step breakdown of the backtracking algorithm:

Start in the leftmost column.
If all queens are placed, return true.
Try all rows in the current column. For each row, do the following:
- If the queen can be placed safely in this row, mark this cell and move to the next column.
- If placing the queen in the current row leads to a solution, return true.
- If placing the queen in the current row does not lead to a solution, unmark this cell (backtrack) and try the next row.
If all rows have been tried and none worked, return false to trigger backtracking.

Code Implementation

import java.util.ArrayList;
import java.util.List;

public class NQueens {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> solutions = new ArrayList<>();
        int[] queens = new int[n];
        solve(0, n, queens, solutions);
        return solutions;
    }

    private void solve(int row, int n, int[] queens, List<List<String>> solutions) {
        if (row == n) {
            solutions.add(generateBoard(queens, n));
            return;
        }
        for (int col = 0; col < n; col++) {
            if (isSafe(row, col, queens)) {
                queens[row] = col;
                solve(row + 1, n, queens, solutions);
            }
        }
    }

    private boolean isSafe(int row, int col, int[] queens) {
        for (int i = 0; i < row; i++) {
            int placedQueenCol = queens[i];
            if (placedQueenCol == col || Math.abs(placedQueenCol - col) == Math.abs(i - row)) {
                return false;
            }
        }
        return true;
    }

    private List<String> generateBoard(int[] queens, int n) {
        List<String> board = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            char[] row = new char[n];
            for (int j = 0; j < n; j++) {
                row[j] = '.';
            }
            row[queens[i]] = 'Q';
            board.add(new String(row));
        }
        return board;
    }

    public static void main(String[] args) {
        NQueens nQueens = new NQueens();
        List<List<String>> solutions = nQueens.solveNQueens(4);
        for (List<String> solution : solutions) {
            for (String row : solution) {
                System.out.println(row);
            }
            System.out.println();
        }
    }
}

Complexity Analysis

The time complexity of the backtracking solution is O(N!), where N is the number of queens. This is because we are trying to place N queens in N rows, and for each queen, we have N choices. The space complexity is O(N) due to the recursion stack and the array used to store the positions of the queens.

Edge Cases

Edge cases include the smallest possible board (n=1) and larger boards where the number of solutions increases significantly. The algorithm handles these cases by ensuring that all possible configurations are explored.

Testing

To test the solution comprehensively, we can use a variety of test cases, from simple (n=1) to complex (n=9). We can also use specific testing frameworks like JUnit to automate the testing process.

Thinking and Problem-Solving Tips

When approaching such problems, it is essential to break down the problem into smaller parts and think about the constraints. Practicing similar problems and studying different algorithms can help improve problem-solving skills.

Conclusion

In this blog post, we discussed the n-queens problem, its significance, and various approaches to solving it. We provided a detailed explanation of the backtracking algorithm and its implementation in Java. Understanding and solving such problems is crucial for developing strong problem-solving skills in computer science.