Intersection of Two Linked Lists in O(m + n) Time Complexity using Java

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:

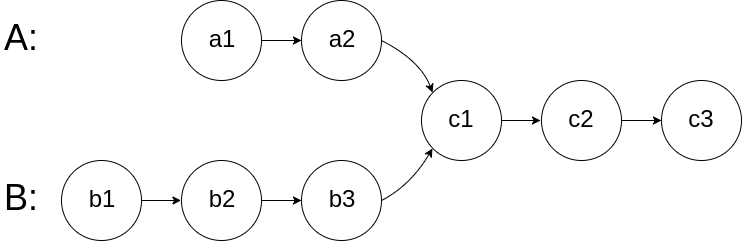
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
listA - The first linked list.
listB - The second linked list.
skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.

The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.

Example 1:

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

Example 2:

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

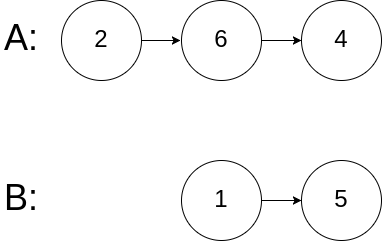
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Constraints:

The number of nodes of listA is in the m.
The number of nodes of listB is in the n.
1 <= m, n <= 3 * 10⁴
1 <= Node.val <= 10⁵
0 <= skipA < m
0 <= skipB < n
intersectVal is 0 if listA and listB do not intersect.
intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

Understanding the Problem

The core challenge of this problem is to identify the node at which two singly linked lists intersect. This problem is significant in various applications, such as finding common paths in network routing or merging data streams. A common pitfall is assuming that the lists intersect at the same position from the head, which is not necessarily true.

Approach

To solve this problem, we need to consider the following steps:

Calculate the lengths of both linked lists.
Align the start of the longer list with the shorter list by skipping the extra nodes.
Traverse both lists simultaneously until we find the intersection node or reach the end of the lists.

Naive Solution

A naive solution would involve using nested loops to compare each node of the first list with each node of the second list. This approach has a time complexity of O(m * n), which is not optimal for large lists.

Optimized Solution

An optimized solution involves using two pointers to traverse the lists. By aligning the pointers at the same distance from the end of the lists, we can find the intersection in O(m + n) time with O(1) space complexity.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

Initialize two pointers, pA and pB, to the heads of headA and headB respectively.
Traverse the lists with the pointers. When a pointer reaches the end of a list, redirect it to the head of the other list.
If the lists intersect, the pointers will meet at the intersection node after at most two passes through the lists.
If the lists do not intersect, the pointers will both reach the end (null) simultaneously.

Code Implementation

// Definition for singly-linked list.
class ListNode {
    int val;
    ListNode next;
    ListNode(int x) {
        val = x;
        next = null;
    }
}

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        // If either head is null, there is no intersection
        if (headA == null || headB == null) return null;

        // Initialize two pointers
        ListNode pA = headA;
        ListNode pB = headB;

        // Traverse the lists
        while (pA != pB) {
            // Move to the next node or switch to the other list's head
            pA = (pA == null) ? headB : pA.next;
            pB = (pB == null) ? headA : pB.next;
        }

        // Either both pointers are null (no intersection) or they meet at the intersection node
        return pA;
    }
}

Complexity Analysis

The time complexity of this solution is O(m + n), where m and n are the lengths of the two linked lists. The space complexity is O(1) since we are only using two additional pointers.

Edge Cases

Consider the following edge cases:

One or both lists are empty: The function should return null.
The lists do not intersect: The function should return null.
The lists intersect at the head: The function should return the head node.

Testing

To test the solution comprehensively, consider the following test cases:

Lists with no intersection.
Lists with intersection at various positions.
Lists of different lengths.

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

Break down the problem into smaller, manageable parts.
Think about edge cases and how to handle them.
Practice similar problems to improve problem-solving skills.

Conclusion

Understanding and solving the intersection of two linked lists is a fundamental problem in computer science. By using an optimized approach, we can achieve efficient solutions that are both time and space efficient. Practice and exploration of similar problems will further enhance your problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources: