Copy List with Random Pointer in Java (O(n) Time Complexity)

A linked list of length n is given such that each node contains an additional random pointer, which could point to any node in the list, or null.

Construct a deep copy of the list. The deep copy should consist of exactly n brand new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list.

For example, if there are two nodes X and Y in the original list, where X.random --> Y, then for the corresponding two nodes x and y in the copied list, x.random --> y.

Return the head of the copied linked list.

The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

• val: an integer representing Node.val
• random_index: the index of the node (range from 0 to n-1) that the random pointer points to, or null if it does not point to any node.

Your code will only be given the head of the original linked list.

 

Example 1:

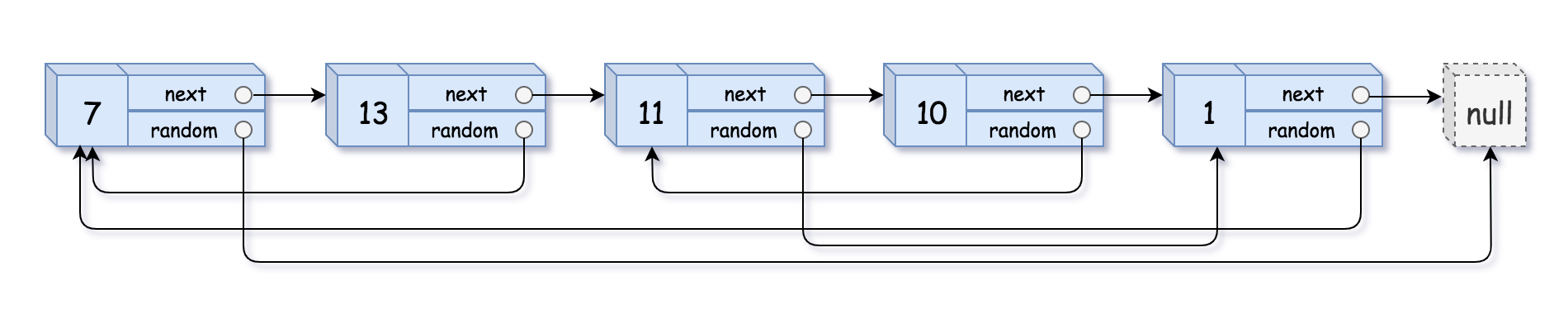
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

Example 2:

Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]

Example 3:

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]

Example 4:

Input: head = []
Output: []
Explanation: The given linked list is empty (null pointer), so return null.

 

Constraints:

• 0 <= n <= 1000
• -10000 <= Node.val <= 10000
• Node.random is null or is pointing to some node in the linked list.

Your algorithm should run in O(n) time and use at most O(n) extra space.

Understanding the Problem

The core challenge of this problem is to create a deep copy of a linked list where each node has an additional random pointer. The deep copy should be a completely new list with no shared references to the original list. This problem is significant in scenarios where data integrity and isolation are crucial, such as in cloning complex data structures or undo mechanisms in applications.

Approach

To solve this problem, we can break it down into three main steps:

1. First, create a copy of each node and insert it right next to the original node in the list.
2. Second, assign the random pointers for the copied nodes.
3. Finally, separate the copied nodes to form the new deep copied list.

Step-by-Step Algorithm

Let's break down the algorithm in detail:

1. Copy Nodes: Traverse the original list and create a new node for each original node. Insert each new node right after its corresponding original node.
2. Assign Random Pointers: Traverse the list again to assign the random pointers for the copied nodes. If the original node's random pointer is not null, set the copied node's random pointer to the copied version of the original node's random pointer.
3. Separate Lists: Finally, traverse the list a third time to separate the original and copied nodes, restoring the original list and forming the new deep copied list.

Code Implementation

class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}

public class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) {
            return null;
        }

        // Step 1: Create a copy of each node and insert it right next to the original node.
        Node current = head;
        while (current != null) {
            Node newNode = new Node(current.val);
            newNode.next = current.next;
            current.next = newNode;
            current = newNode.next;
        }

        // Step 2: Assign random pointers for the copied nodes.
        current = head;
        while (current != null) {
            if (current.random != null) {
                current.next.random = current.random.next;
            }
            current = current.next.next;
        }

        // Step 3: Separate the copied nodes to form the new deep copied list.
        current = head;
        Node newHead = head.next;
        Node copy = newHead;
        while (current != null) {
            current.next = current.next.next;
            if (copy.next != null) {
                copy.next = copy.next.next;
            }
            current = current.next;
            copy = copy.next;
        }

        return newHead;
    }
}

Complexity Analysis

The time complexity of this algorithm is O(n) because we traverse the list three times, each taking linear time. The space complexity is also O(n) due to the space required for the new nodes.

Edge Cases

Consider the following edge cases:

• An empty list (head is null).
• A list where all random pointers are null.
• A list where random pointers form a cycle.

Our algorithm handles these cases effectively by ensuring that the deep copy is accurate and isolated from the original list.

Testing

To test the solution comprehensively, consider the following test cases:

• Simple lists with no random pointers.
• Lists with random pointers pointing to various nodes, including themselves.
• Edge cases such as empty lists and single-node lists.

Conclusion

Understanding and solving the "Copy List with Random Pointer" problem is crucial for mastering deep copy techniques in linked lists. By breaking down the problem and following a structured approach, we can create an efficient solution that runs in O(n) time and uses O(n) extra space.

Additional Resources

For further reading and practice problems, consider the following resources:

• LeetCode Problem
• Deep Copy - Wikipedia
• GeeksforGeeks Article