You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
Input: list1 =[2, 4, 3], list2 =[5, 6, 4]Output:[7, 0, 8]Explanation: 342 + 465 = 807
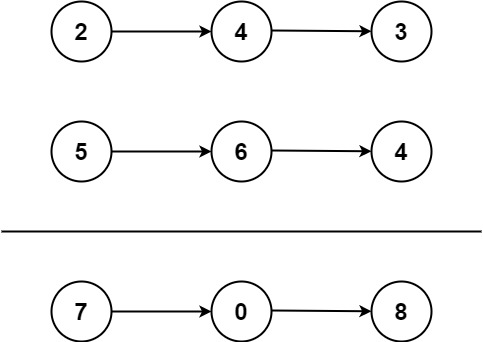
Example 2:
Input: list1 =[9,9,9,9,9,9,9], list2 =[9,9,9,9]Output:[8,9,9,9,0,0,0,1]Explanation: 9999999 + 9999 = 10009998
The core challenge of this problem is to handle the addition of two numbers represented as linked lists, where each node contains a single digit and the digits are stored in reverse order. This means the least significant digit comes first. The task is to add these two numbers and return the result as a linked list in the same reverse order format.
This problem is significant in scenarios where numbers are too large to be handled by standard data types, and thus, they are stored in a linked list format. Common applications include arbitrary-precision arithmetic and certain cryptographic algorithms.
Potential pitfalls include handling the carry-over during addition and ensuring that the resulting linked list correctly represents the sum without leading zeros (except for the number 0 itself).
To solve this problem, we can use a straightforward approach by iterating through both linked lists simultaneously, adding corresponding digits along with any carry from the previous addition. If one list is shorter, we continue with the longer list while considering the carry.
Here is a step-by-step approach:
Let's break down the algorithm step-by-step:
// Definition for singly-linked list.
class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}
public class AddTwoNumbers {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// Initialize a dummy node to act as the head of the result list
ListNode dummyHead = new ListNode(0);
ListNode p = l1, q = l2, current = dummyHead;
int carry = 0;
// Loop through both lists until both are null and there is no carry
while (p != null || q != null) {
// Get the values of the current nodes, or 0 if the node is null
int x = (p != null) ? p.val : 0;
int y = (q != null) ? q.val : 0;
// Calculate the sum of the values and the carry
int sum = carry + x + y;
// Update the carry for the next iteration
carry = sum / 10;
// Create a new node with the digit value of the current sum modulo 10
current.next = new ListNode(sum % 10);
// Move the current pointer to the next node
current = current.next;
// Move the input list pointers to their next nodes if they exist
if (p != null) p = p.next;
if (q != null) q = q.next;
}
// If there is a carry left, create a new node with the carry value
if (carry > 0) {
current.next = new ListNode(carry);
}
// Return the result list, starting from the next node of the dummy head
return dummyHead.next;
}
}
The time complexity of this approach is O(max(m, n)), where m and n are the lengths of the two input linked lists. This is because we iterate through both lists once. The space complexity is O(max(m, n)) as well, due to the space required for the result linked list.
Potential edge cases include:
Examples of edge cases and their expected outputs:
Input: list1 = [0], list2 = [0] Output: [0] Input: list1 = [9,9,9], list2 = [1] Output: [0,0,0,1]
To test the solution comprehensively, consider a variety of test cases:
Testing frameworks like JUnit can be used to automate the testing process.
When approaching such problems, consider the following tips:
In this blog post, we discussed how to add two numbers represented as linked lists in Java. We covered the problem definition, approach, algorithm, code implementation, complexity analysis, edge cases, and testing. Understanding and solving such problems is crucial for developing strong problem-solving skills and preparing for technical interviews.
We encourage you to practice and explore further to solidify your understanding.
For further reading and practice problems, consider the following resources:
Our interactive tutorials and AI-assisted learning will help you master problem-solving skills and teach you the algorithms to know for coding interviews.
Start Coding for FREE