Palindrome Linked List in C++ (O(n) Time and O(1) Space)

Given the head of a singly linked list, return true if it is a palindrome.

 

Example 1:

Input: head = [1,2,2,1]
Output: true

Example 2:

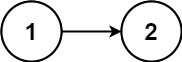
Input: head = [1,2]
Output: false

 

Constraints:

• The number of nodes in the list is in the range [1, 105].
• 0 <= Node.val <= 9

 

Follow up: Could you do it in O(n) time and O(1) space?

Understanding the Problem

The core challenge of this problem is to determine if the values in a singly linked list form a palindrome. A palindrome is a sequence that reads the same backward as forward. This problem is significant in various applications such as text processing, data validation, and more.

Potential pitfalls include handling edge cases like an empty list or a list with a single node, and ensuring the solution is efficient in both time and space.

Approach

To solve this problem, we can consider the following approaches:

Naive Approach

A naive solution would involve copying the linked list values into an array, then checking if the array is a palindrome. This approach is straightforward but requires O(n) space, which is not optimal.

Optimized Approach

To achieve O(n) time and O(1) space, we can use the following steps:

1. Find the middle of the linked list using the slow and fast pointer technique.
2. Reverse the second half of the linked list.
3. Compare the first half and the reversed second half of the list.
4. Restore the original list structure (optional).

Algorithm

Let's break down the optimized algorithm step-by-step:

Step 1: Find the Middle

Use two pointers, slow and fast. Move slow by one step and fast by two steps. When fast reaches the end, slow will be at the middle.

Step 2: Reverse the Second Half

Reverse the nodes starting from the middle to the end of the list.

Step 3: Compare Halves

Compare the values of the nodes in the first half with the values in the reversed second half.

Step 4: Restore the List

Optionally, reverse the second half again to restore the original list structure.

Code Implementation

#include <iostream>
using namespace std;

// Definition for singly-linked list.
struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (!head || !head->next) return true;

        // Step 1: Find the middle of the linked list
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }

        // Step 2: Reverse the second half of the linked list
        ListNode *prev = nullptr, *curr = slow, *next = nullptr;
        while (curr) {
            next = curr->next;
            curr->next = prev;
            prev = curr;
            curr = next;
        }

        // Step 3: Compare the first half and the reversed second half
        ListNode *firstHalf = head, *secondHalf = prev;
        while (secondHalf) {
            if (firstHalf->val != secondHalf->val) return false;
            firstHalf = firstHalf->next;
            secondHalf = secondHalf->next;
        }

        // Optional Step 4: Restore the original list (not required for the problem)
        // Reverse the second half again to restore the list

        return true;
    }
};

Complexity Analysis

The time complexity of this approach is O(n) because we traverse the list a constant number of times. The space complexity is O(1) because we only use a few pointers for the operations.

Edge Cases

Consider the following edge cases:

• Single node list: [1]
• Two nodes, not a palindrome: [1, 2]
• Two nodes, a palindrome: [1, 1]

These cases should be handled correctly by the algorithm.

Testing

To test the solution comprehensively, consider a variety of test cases:

• Empty list
• Single node list
• Even number of nodes, palindrome
• Even number of nodes, not a palindrome
• Odd number of nodes, palindrome
• Odd number of nodes, not a palindrome

Thinking and Problem-Solving Tips

When approaching such problems, consider breaking down the problem into smaller steps and think about how to optimize both time and space. Practice similar problems to improve your problem-solving skills.

Conclusion

In this blog post, we discussed how to determine if a singly linked list is a palindrome using an optimized approach with O(n) time and O(1) space complexity. Understanding and solving such problems is crucial for improving algorithmic thinking and coding skills.

Additional Resources

For further reading and practice, consider the following resources:

• LeetCode: Palindrome Linked List
• GeeksforGeeks: Check if a singly linked list is palindrome
• Coding Ninjas: Palindrome Linked List