N Queens Problem in C++ with Time Complexity Analysis

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, and is represented as an array containing the column for each row of the matrix.

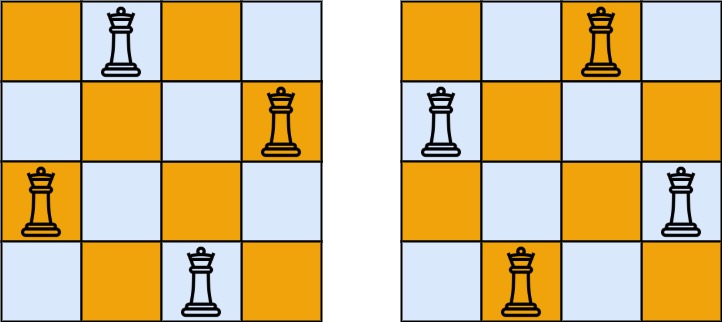
Example:

Input: n = 4
Output: [[1, 3, 0, 2], [2, 0, 3, 1]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Constraints:

1 <= n <= 9

Understanding the Problem

The core challenge of the N Queens problem is to place n queens on an n x n chessboard such that no two queens can attack each other. This means no two queens can be in the same row, column, or diagonal.

This problem is significant in the field of combinatorial optimization and has applications in various domains such as parallel computing, network design, and more.

Potential pitfalls include misunderstanding the constraints of the problem, such as ensuring that no two queens share the same diagonal.

Approach

To solve the N Queens problem, we can use a backtracking approach. The idea is to place queens one by one in different columns, starting from the leftmost column. When placing a queen, we check for clashes with already placed queens. If a clash is found, we backtrack and try the next column.

Naive Solution

A naive solution would involve generating all possible configurations of queens on the board and then checking each configuration for validity. This approach is not optimal due to its high time complexity.

Optimized Solution

The optimized solution uses backtracking to place queens one by one and checks for validity at each step. This reduces the number of configurations that need to be checked.

Algorithm

Here is a step-by-step breakdown of the backtracking algorithm:

Start in the leftmost column.
If all queens are placed, return true.
Try all rows in the current column. For each row, do the following:
- If the queen can be placed safely in this row, mark this cell and move to the next column.
- If placing the queen in the current row leads to a solution, return true.
- If placing the queen in the current row does not lead to a solution, unmark this cell (backtrack) and try the next row.
If all rows have been tried and none worked, return false to trigger backtracking.

Code Implementation

#include <iostream>
#include <vector>

using namespace std;

// Function to check if a queen can be placed on board[row][col]
bool isSafe(vector<int> &board, int row, int col) {
    for (int i = 0; i < row; ++i) {
        if (board[i] == col || abs(board[i] - col) == abs(i - row)) {
            return false;
        }
    }
    return true;
}

// Recursive utility function to solve N Queens problem
void solveNQueensUtil(int n, int row, vector<int> &board, vector<vector<int>> &solutions) {
    if (row == n) {
        solutions.push_back(board);
        return;
    }
    for (int col = 0; col < n; ++col) {
        if (isSafe(board, row, col)) {
            board[row] = col;
            solveNQueensUtil(n, row + 1, board, solutions);
            board[row] = -1; // Backtrack
        }
    }
}

// Function to solve N Queens problem
vector<vector<int>> solveNQueens(int n) {
    vector<vector<int>> solutions;
    vector<int> board(n, -1);
    solveNQueensUtil(n, 0, board, solutions);
    return solutions;
}

int main() {
    int n = 4;
    vector<vector<int>> solutions = solveNQueens(n);
    for (const auto &solution : solutions) {
        for (int col : solution) {
            cout << col << " ";
        }
        cout << endl;
    }
    return 0;
}

Complexity Analysis

The time complexity of the backtracking solution is O(N!), where N is the number of queens. This is because we are trying to place each queen in N possible positions, and for each position, we recursively try to place the next queen.

The space complexity is O(N) for the board array used to store the positions of the queens.

Edge Cases

Edge cases include:

n = 1: The solution is trivial as there is only one queen.
n = 2 or n = 3: There are no solutions for these values of n.

Our algorithm handles these cases by naturally returning an empty list of solutions when no valid configurations are found.

Testing

To test the solution comprehensively, we should include a variety of test cases:

Simple cases like n = 1, 2, 3.
Standard cases like n = 4, 5, 6.
Edge cases like n = 9 (maximum constraint).

We can use testing frameworks like Google Test for C++ to automate and manage our test cases.

Thinking and Problem-Solving Tips

When approaching such problems, it is essential to:

Understand the problem constraints and requirements thoroughly.
Break down the problem into smaller, manageable parts.
Consider different approaches and analyze their time and space complexities.
Practice solving similar problems to improve problem-solving skills.

Conclusion

The N Queens problem is a classic example of a combinatorial optimization problem that can be efficiently solved using backtracking. Understanding and solving such problems helps in developing strong problem-solving skills and a deep understanding of algorithms.

We encourage readers to practice and explore further to master these concepts.