Copy List with Random Pointer in C++ (O(n) Time Complexity)

A linked list of length n is given such that each node contains an additional random pointer, which could point to any node in the list, or null.

Construct a deep copy of the list. The deep copy should consist of exactly n brand new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list.

For example, if there are two nodes X and Y in the original list, where X.random --> Y, then for the corresponding two nodes x and y in the copied list, x.random --> y.

Return the head of the copied linked list.

The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

val: an integer representing Node.val
random_index: the index of the node (range from 0 to n-1) that the random pointer points to, or null if it does not point to any node.

Your code will only be given the head of the original linked list.

Example 1:

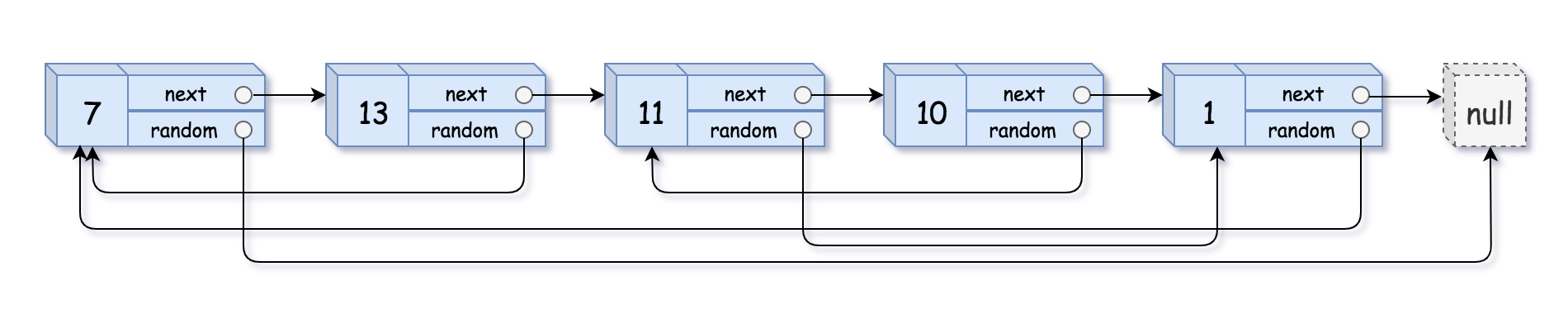
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

Example 2:

Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]

Example 3:

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]

Example 4:

Input: head = []
Output: []
Explanation: The given linked list is empty (null pointer), so return null.

Constraints:

0 <= n <= 1000
-10000 <= Node.val <= 10000
Node.random is null or is pointing to some node in the linked list.

Note:

Your algorithm should run in O(n) time and use at most O(n) extra space.

Understanding the Problem

The core challenge of this problem is to create a deep copy of a linked list where each node has an additional random pointer. The deep copy should be a completely new list with no shared nodes with the original list. This problem is significant in scenarios where data structures with complex relationships need to be duplicated without affecting the original structure.

Approach

To solve this problem, we can use a three-step approach:

Interweaving the original list with copied nodes: Create new nodes and insert them right after each original node.
Assigning random pointers: Set the random pointers of the new nodes using the interwoven structure.
Restoring the original list and extracting the copied list: Separate the interwoven list into the original and the copied list.

Algorithm

Let's break down the algorithm step-by-step:

Traverse the original list and create new nodes. Insert each new node right after its corresponding original node.
Traverse the interwoven list and set the random pointers of the new nodes.
Separate the interwoven list into the original list and the copied list.

Code Implementation

// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = nullptr;
        random = nullptr;
    }
};

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if (!head) return nullptr;

        // Step 1: Create new nodes and interweave them with the original nodes
        Node* curr = head;
        while (curr) {
            Node* newNode = new Node(curr->val);
            newNode->next = curr->next;
            curr->next = newNode;
            curr = newNode->next;
        }

        // Step 2: Assign random pointers to the new nodes
        curr = head;
        while (curr) {
            if (curr->random) {
                curr->next->random = curr->random->next;
            }
            curr = curr->next->next;
        }

        // Step 3: Separate the interwoven list into original and copied lists
        curr = head;
        Node* newHead = head->next;
        Node* copyCurr = newHead;
        while (curr) {
            curr->next = curr->next->next;
            if (copyCurr->next) {
                copyCurr->next = copyCurr->next->next;
            }
            curr = curr->next;
            copyCurr = copyCurr->next;
        }

        return newHead;
    }
};

Complexity Analysis

The time complexity of this approach is O(n) because we traverse the list a constant number of times. The space complexity is also O(n) due to the space required for the new nodes.

Edge Cases

Consider the following edge cases:

An empty list (head is null).
A list where all random pointers are null.
A list where random pointers form a cycle.

Testing

To test the solution comprehensively, consider the following test cases:

Simple lists with no random pointers.
Lists with random pointers pointing to various nodes.
Edge cases as mentioned above.

Thinking and Problem-Solving Tips

When approaching such problems, it's essential to:

Understand the problem requirements and constraints thoroughly.
Break down the problem into smaller, manageable steps.
Consider edge cases and test your solution against them.
Practice similar problems to improve problem-solving skills.

Conclusion

In this blog post, we discussed how to create a deep copy of a linked list with random pointers. We explored the problem definition, approach, algorithm, and provided a detailed C++ implementation. Understanding and solving such problems is crucial for mastering data structures and algorithms.

Additional Resources

For further reading and practice, consider the following resources: