You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
Input: list1 =[2, 4, 3], list2 =[5, 6, 4]Output:[7, 0, 8]Explanation: 342 + 465 = 807
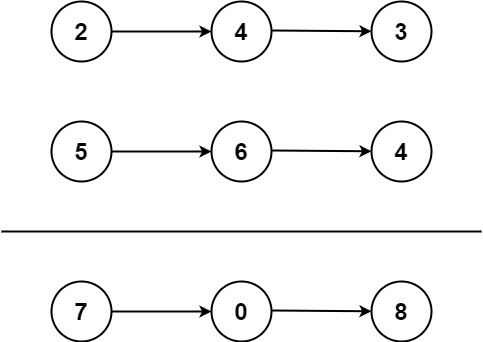
Example 2:
Input: list1 =[9,9,9,9,9,9,9], list2 =[9,9,9,9]Output:[8,9,9,9,0,0,0,1]Explanation: 9999999 + 9999 = 10009998
The core challenge of this problem is to handle the addition of two numbers represented as linked lists, where each node contains a single digit. The digits are stored in reverse order, which means the least significant digit comes first. This is similar to how we perform addition manually, starting from the rightmost digit and moving to the left.
Common applications of this problem include scenarios where large numbers need to be processed that cannot fit into standard data types, such as in financial calculations or scientific computations.
Potential pitfalls include handling the carry-over correctly and ensuring that the resulting linked list is properly constructed without any leading zeros (except for the number 0 itself).
To solve this problem, we can use a straightforward approach that mimics the manual addition process:
This approach ensures that we correctly handle the addition of digits and the carry-over, resulting in the correct sum represented as a linked list.
Here is a step-by-step breakdown of the algorithm:
#include <iostream>
using namespace std;
// Definition for singly-linked list.
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
// Initialize a dummy node to act as the head of the result linked list
ListNode* dummy = new ListNode();
ListNode* current = dummy;
int carry = 0;
// Traverse both linked lists
while (l1 != nullptr || l2 != nullptr || carry != 0) {
// Get the values of the current nodes (or 0 if the list is exhausted)
int val1 = (l1 != nullptr) ? l1->val : 0;
int val2 = (l2 != nullptr) ? l2->val : 0;
// Calculate the sum and update the carry
int sum = val1 + val2 + carry;
carry = sum / 10;
// Create a new node with the value of sum % 10
current->next = new ListNode(sum % 10);
current = current->next;
// Move to the next nodes
if (l1 != nullptr) l1 = l1->next;
if (l2 != nullptr) l2 = l2->next;
}
// Return the next node of the dummy node as the head of the result linked list
return dummy->next;
}
};
// Helper function to print the linked list
void printList(ListNode* node) {
while (node != nullptr) {
cout << node->val << " ";
node = node->next;
}
cout << endl;
}
// Main function to test the solution
int main() {
// Create the first linked list: 2 -> 4 -> 3
ListNode* l1 = new ListNode(2);
l1->next = new ListNode(4);
l1->next->next = new ListNode(3);
// Create the second linked list: 5 -> 6 -> 4
ListNode* l2 = new ListNode(5);
l2->next = new ListNode(6);
l2->next->next = new ListNode(4);
// Create a solution object
Solution solution;
// Add the two numbers
ListNode* result = solution.addTwoNumbers(l1, l2);
// Print the result linked list
printList(result);
return 0;
}
The time complexity of this approach is O(max(n, m)), where n and m are the lengths of the input linked lists. This is because we traverse both linked lists once. The space complexity is O(max(n, m)) as well, due to the space required for the result linked list.
Potential edge cases include:
Our algorithm handles these edge cases by checking for null pointers and ensuring the carry is correctly managed.
To test the solution comprehensively, we can use a variety of test cases:
We can use the provided helper function to print the linked list and verify the results manually.
When approaching such problems, it is essential to:
Practicing similar problems and studying algorithms can help improve problem-solving skills.
In this blog post, we discussed how to solve the problem of adding two numbers represented as linked lists. We covered the problem definition, approach, algorithm, code implementation, complexity analysis, edge cases, and testing. Understanding and solving such problems is crucial for developing strong problem-solving skills and improving coding proficiency.
We encourage readers to practice and explore further to enhance their understanding and skills.
For further reading and practice, consider the following resources: