Algocademy Logo

Course Outline

Symmetric Tree in Python (Time Complexity: O(n))


Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

 

Example 1:

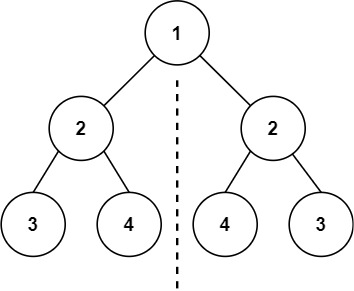
Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

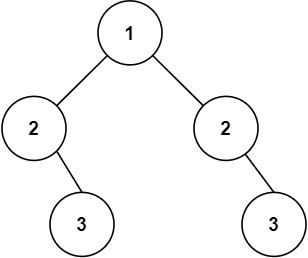
Input: root = [1,2,2,null,3,null,3]
Output: false

 

Constraints:

  • The number of nodes in the tree is in the range [1, 1000].
  • -100 <= Node.val <= 100

 

Follow up: Could you solve it both recursively and iteratively?

Understanding the Problem

The core challenge of this problem is to determine if a binary tree is symmetric around its center. This means that the left subtree should be a mirror reflection of the right subtree.

Common applications of this problem include validating the structure of data in hierarchical systems and ensuring balanced data distribution in tree-based structures.

Potential pitfalls include misunderstanding the symmetry concept and not handling null nodes correctly.

Approach

To solve this problem, we can use two main approaches: recursive and iterative.

Recursive Approach

In the recursive approach, we define a helper function that checks if two trees are mirror images of each other. This function will be called with the left and right children of the root node.

Steps:

  • Check if both nodes are null. If yes, return True.
  • If one of the nodes is null, return False.
  • Check if the values of the nodes are equal.
  • Recursively check if the left subtree of the left node is a mirror of the right subtree of the right node and vice versa.

Iterative Approach

In the iterative approach, we use a queue to perform a level-order traversal and compare nodes at each level.

Steps:

  • Initialize a queue and add the left and right children of the root node.
  • While the queue is not empty, pop two nodes and compare them.
  • If both nodes are null, continue to the next iteration.
  • If one of the nodes is null or their values are not equal, return False.
  • Add the children of the nodes to the queue in the order that ensures symmetry.

Algorithm

Recursive Algorithm

def is_symmetric(root):
    def is_mirror(left, right):
        # If both nodes are null, they are mirrors
        if not left and not right:
            return True
        # If one of the nodes is null, they are not mirrors
        if not left or not right:
            return False
        # Check if the current nodes are equal and their subtrees are mirrors
        return (left.val == right.val and
                is_mirror(left.left, right.right) and
                is_mirror(left.right, right.left))
    
    # Start the recursion with the left and right children of the root
    return is_mirror(root.left, root.right)

Iterative Algorithm

from collections import deque

def is_symmetric(root):
    if not root:
        return True
    
    queue = deque([(root.left, root.right)])
    
    while queue:
        left, right = queue.popleft()
        
        # If both nodes are null, continue
        if not left and not right:
            continue
        # If one of the nodes is null, they are not mirrors
        if not left or not right:
            return False
        # If the values are not equal, they are not mirrors
        if left.val != right.val:
            return False
        
        # Add the children in the order that ensures symmetry
        queue.append((left.left, right.right))
        queue.append((left.right, right.left))
    
    return True

Complexity Analysis

For both the recursive and iterative approaches, the time complexity is O(n), where n is the number of nodes in the tree. This is because we visit each node once.

The space complexity for the recursive approach is O(h), where h is the height of the tree, due to the recursion stack. For the iterative approach, the space complexity is O(n) due to the queue.

Edge Cases

Consider the following edge cases:

  • An empty tree (should return True).
  • A tree with only one node (should return True).
  • A tree with null nodes at various positions.

Testing

To test the solution comprehensively, consider the following test cases:

def test_is_symmetric():
    # Test case 1: Symmetric tree
    root1 = TreeNode(1)
    root1.left = TreeNode(2)
    root1.right = TreeNode(2)
    root1.left.left = TreeNode(3)
    root1.left.right = TreeNode(4)
    root1.right.left = TreeNode(4)
    root1.right.right = TreeNode(3)
    assert is_symmetric(root1) == True
    
    # Test case 2: Asymmetric tree
    root2 = TreeNode(1)
    root2.left = TreeNode(2)
    root2.right = TreeNode(2)
    root2.left.right = TreeNode(3)
    root2.right.right = TreeNode(3)
    assert is_symmetric(root2) == False
    
    # Test case 3: Single node tree
    root3 = TreeNode(1)
    assert is_symmetric(root3) == True
    
    # Test case 4: Empty tree
    root4 = None
    assert is_symmetric(root4) == True

test_is_symmetric()

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

  • Break down the problem into smaller subproblems.
  • Think about the properties of the data structure (e.g., symmetry in trees).
  • Consider both recursive and iterative solutions.
  • Write pseudocode to outline your approach before coding.

Conclusion

Understanding and solving the symmetric tree problem helps in grasping tree traversal techniques and recursion. Practice with different tree problems to improve your problem-solving skills.

Additional Resources