The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, and is represented as an array containing the column for each row of the matrix.
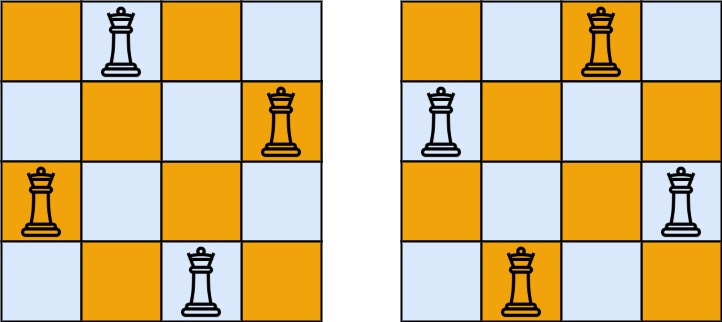
Example:
Input: n = 4 Output: [[1, 3, 0, 2], [2, 0, 3, 1]] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Constraints:
1 <= n <= 9The core challenge of the n-queens problem is to place n queens on an n x n chessboard such that no two queens can attack each other. This means no two queens can be in the same row, column, or diagonal.
This problem is significant in the field of combinatorial optimization and has applications in various fields such as algorithm design, artificial intelligence, and operations research.
Potential pitfalls include misunderstanding the constraints of the problem, such as ensuring that no two queens share the same diagonal.
To solve the n-queens problem, we can use a backtracking approach. Backtracking is a general algorithm for finding all (or some) solutions to computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot possibly be completed to a valid solution.
A naive solution would involve generating all possible arrangements of queens on the board and then checking each arrangement to see if it meets the constraints. This approach is not optimal due to its high time complexity.
An optimized solution involves using backtracking to place queens one by one in different columns, starting from the leftmost column. When placing a queen, we check for clashes with already placed queens. If a clash is found, we backtrack and try the next position.
Here is a step-by-step breakdown of the backtracking algorithm:
def solveNQueens(n):
def is_safe(board, row, col):
# Check this row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, n, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solve(board, col):
# base case: If all queens are placed
if col >= n:
solution = []
for i in range(n):
for j in range(n):
if board[i][j] == 1:
solution.append(j)
results.append(solution)
return True
res = False
for i in range(n):
if is_safe(board, i, col):
board[i][col] = 1
res = solve(board, col + 1) or res
board[i][col] = 0 # backtrack
return res
results = []
board = [[0 for _ in range(n)] for _ in range(n)]
solve(board, 0)
return results
# Example usage:
print(solveNQueens(4))
The time complexity of the backtracking solution is O(N!), where N is the number of queens. This is because we are trying to place each queen in N possible positions, and for each position, we recursively try to place the next queen.
The space complexity is O(N^2) due to the board representation.
Edge cases include the smallest possible board (n=1) and larger boards where the solution space grows exponentially. The algorithm handles these cases by design, as it systematically explores all possible placements.
To test the solution comprehensively, we can use a variety of test cases:
We can use Python's unittest framework to automate these tests.
When approaching such problems, it's essential to break down the problem into smaller parts and think about the constraints. Practicing similar problems and studying different algorithms can significantly improve problem-solving skills.
The n-queens problem is a classic example of a constraint satisfaction problem that can be efficiently solved using backtracking. Understanding and solving such problems is crucial for developing strong algorithmic thinking and problem-solving skills.