Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).
Assume a BST is defined as follows:
Example 1:
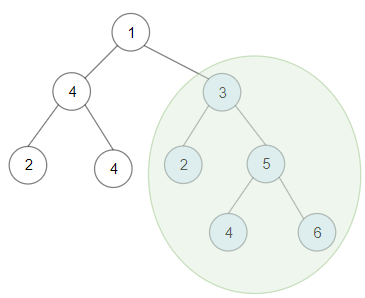
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6] Output: 20 Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
Example 2:
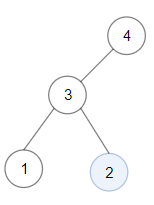
Input: root = [4,3,null,1,2] Output: 2 Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
Example 3:
Input: root = [-4,-2,-5] Output: 0 Explanation: All values are negatives. Return an empty BST.
Example 4:
Input: root = [2,1,3] Output: 6
Example 5:
Input: root = [5,4,8,3,null,6,3] Output: 7
Constraints:
40000 nodes..[-4 * 10^4 , 4 * 10^4].The core challenge of this problem is to identify the largest sum of keys in any subtree that is a valid Binary Search Tree (BST). A BST is defined by the properties that all nodes in the left subtree are less than the root, and all nodes in the right subtree are greater than the root. Both subtrees must also be BSTs.
This problem is significant in various applications such as database indexing, where BST properties are used to maintain sorted data for efficient retrieval.
Potential pitfalls include incorrectly identifying BSTs or not considering all possible subtrees.
To solve this problem, we need to traverse the tree and check each subtree to see if it is a BST. A naive approach would involve checking each subtree individually, which would be inefficient. Instead, we can use a post-order traversal to gather information about each subtree and determine if it forms a BST.
We will use a helper function that returns multiple values for each node: whether the subtree is a BST, the sum of the subtree, the minimum value in the subtree, and the maximum value in the subtree. This information will help us efficiently determine the maximum sum of any BST subtree.
1. Define a helper function that performs a post-order traversal of the tree.
2. For each node, recursively check its left and right subtrees.
3. Gather information about whether the left and right subtrees are BSTs, their sums, and their min/max values.
4. Use this information to determine if the current subtree is a BST and calculate its sum if it is.
5. Keep track of the maximum sum encountered during the traversal.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def maxSumBST(self, root: TreeNode) -> int:
self.max_sum = 0
def post_order(node):
if not node:
# Return a tuple (isBST, sum, min, max)
return (True, 0, float('inf'), float('-inf'))
left_is_bst, left_sum, left_min, left_max = post_order(node.left)
right_is_bst, right_sum, right_min, right_max = post_order(node.right)
if left_is_bst and right_is_bst and left_max < node.val < right_min:
# Current subtree is a BST
current_sum = left_sum + right_sum + node.val
self.max_sum = max(self.max_sum, current_sum)
return (True, current_sum, min(left_min, node.val), max(right_max, node.val))
else:
# Current subtree is not a BST
return (False, 0, float('-inf'), float('inf'))
post_order(root)
return self.max_sum
The time complexity of this approach is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once during the post-order traversal.
The space complexity is O(h), where h is the height of the tree. This is due to the recursion stack used during the traversal.
1. An empty tree should return 0.
2. Trees with all negative values should return 0, as the best BST in this case is an empty tree.
3. Trees with only one node should return the value of that node.
To test the solution comprehensively, consider the following test cases:
Using a testing framework like unittest or pytest can help automate and validate these test cases.
1. Break down the problem into smaller subproblems.
2. Use helper functions to manage complex logic.
3. Practice similar problems to improve your understanding of tree traversals and BST properties.
Understanding and solving problems related to BSTs is crucial for efficient data management and retrieval. By practicing such problems, you can improve your problem-solving skills and gain a deeper understanding of tree data structures.