Linked List Cycle - Time Complexity: O(n), Space Complexity: O(1) - Python

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

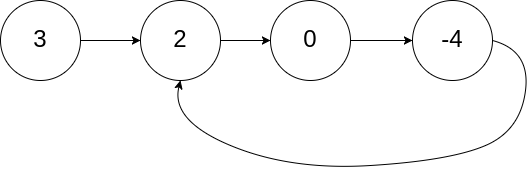
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

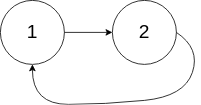
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10⁴].
-10⁵ <= Node.val <= 10⁵
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Understanding the Problem

The core challenge of this problem is to detect if a linked list contains a cycle. A cycle occurs when a node's next pointer points back to a previous node, creating a loop. This problem is significant in various applications such as detecting infinite loops in programs, network routing, and more.

Potential pitfalls include misunderstanding the cycle detection mechanism and not handling edge cases like an empty list or a single node without a cycle.

Approach

To solve this problem, we can use two main approaches:

Naive Approach: Use a hash set to keep track of visited nodes. If we encounter a node that is already in the set, a cycle exists. This approach uses O(n) space.
Optimized Approach: Use Floyd's Tortoise and Hare algorithm, which uses two pointers moving at different speeds. If they meet, a cycle exists. This approach uses O(1) space.

Naive Approach

In the naive approach, we traverse the linked list and store each visited node in a hash set. If we encounter a node that is already in the set, we return true, indicating a cycle. Otherwise, we return false if we reach the end of the list.

Optimized Approach: Floyd's Tortoise and Hare Algorithm

In this approach, we use two pointers, slow (tortoise) and fast (hare). The slow pointer moves one step at a time, while the fast pointer moves two steps at a time. If there is a cycle, the fast pointer will eventually meet the slow pointer. If the fast pointer reaches the end of the list, there is no cycle.

Algorithm

Naive Approach

Initialize an empty hash set.
Traverse the linked list.
If the current node is in the hash set, return true.
Add the current node to the hash set.
If the traversal ends, return false.

Floyd's Tortoise and Hare Algorithm

Initialize two pointers, slow and fast, both pointing to the head.
Move slow one step and fast two steps at a time.
If slow and fast meet, return true.
If fast reaches the end, return false.

Code Implementation

Naive Approach

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

def hasCycle(head):
    visited = set()
    current = head
    while current:
        if current in visited:
            return True
        visited.add(current)
        current = current.next
    return False

Floyd's Tortoise and Hare Algorithm

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

def hasCycle(head):
    if not head or not head.next:
        return False
    slow = head
    fast = head.next
    while slow != fast:
        if not fast or not fast.next:
            return False
        slow = slow.next
        fast = fast.next.next
    return True

Complexity Analysis

Naive Approach:

Time Complexity: O(n) - We traverse the list once.
Space Complexity: O(n) - We store each visited node in a hash set.

Floyd's Tortoise and Hare Algorithm:

Time Complexity: O(n) - In the worst case, we traverse the list once.
Space Complexity: O(1) - We use only two pointers.

Edge Cases

Consider the following edge cases:

An empty list (head is None).
A single node without a cycle.
A single node with a cycle (node points to itself).
A list with multiple nodes and no cycle.
A list with multiple nodes and a cycle.

Testing

To test the solution comprehensively, consider the following test cases:

def test_hasCycle():
    # Test case 1: Empty list
    assert hasCycle(None) == False

    # Test case 2: Single node without cycle
    node1 = ListNode(1)
    assert hasCycle(node1) == False

    # Test case 3: Single node with cycle
    node1.next = node1
    assert hasCycle(node1) == True

    # Test case 4: Multiple nodes without cycle
    node1 = ListNode(1)
    node2 = ListNode(2)
    node1.next = node2
    assert hasCycle(node1) == False

    # Test case 5: Multiple nodes with cycle
    node3 = ListNode(3)
    node4 = ListNode(4)
    node1.next = node2
    node2.next = node3
    node3.next = node4
    node4.next = node2
    assert hasCycle(node1) == True

test_hasCycle()

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

Understand the problem requirements and constraints thoroughly.
Think about different approaches and their trade-offs.
Start with a simple solution and then optimize it.
Consider edge cases and test your solution comprehensively.

Conclusion

Detecting a cycle in a linked list is a common problem with applications in various fields. Understanding different approaches and their trade-offs is crucial for solving such problems efficiently. Practice and exploration of similar problems can help improve problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources: