Algocademy Logo

Course Outline

Video 1 of 2

Largest Rectangle in Histogram - Python Solution with O(n) Time Complexity


Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

 

Example 1:

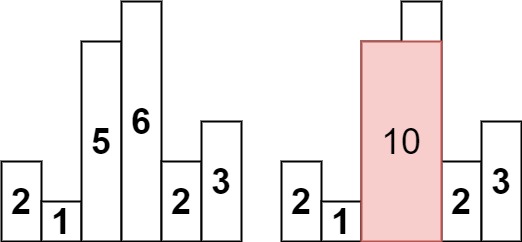
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

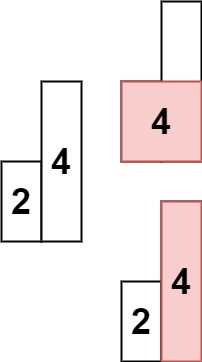
Input: heights = [2,4]
Output: 4

 

Constraints:

  • 1 <= heights.length <= 105
  • 0 <= heights[i] <= 104

Understanding the Problem

The core challenge of this problem is to find the largest rectangular area that can be formed within the histogram. This problem is significant in various fields such as computer graphics, data visualization, and computational geometry. A common pitfall is to attempt a brute-force solution, which would be inefficient for large inputs.

Approach

To solve this problem efficiently, we can use a stack-based approach. The idea is to maintain a stack of indices of the histogram's bars. We iterate through each bar and use the stack to keep track of the bars that are not yet processed. This allows us to calculate the maximum area in O(n) time complexity.

Naive Solution

A naive solution would involve checking every possible rectangle by iterating through each pair of bars and calculating the area. This approach would have a time complexity of O(n^2), which is not feasible for large inputs.

Optimized Solution

The optimized solution uses a stack to keep track of the indices of the bars. We iterate through the histogram, and for each bar, we pop from the stack until we find a bar that is shorter than the current bar. For each popped bar, we calculate the area with the popped bar as the smallest (or minimum height) bar. This ensures that we calculate the maximum area for each bar efficiently.

Algorithm

Here is a step-by-step breakdown of the stack-based algorithm:

  1. Initialize an empty stack and set max_area to 0.
  2. Iterate through each bar in the histogram.
  3. For each bar, pop from the stack while the current bar is shorter than the bar at the index stored at the top of the stack.
  4. For each popped bar, calculate the area with the popped bar as the smallest bar and update max_area if the calculated area is larger.
  5. Push the current bar's index onto the stack.
  6. After iterating through all bars, pop the remaining bars from the stack and calculate the area for each.

Code Implementation

def largestRectangleArea(heights):
    # Initialize an empty stack and max_area to 0
    stack = []
    max_area = 0
    index = 0

    while index < len(heights):
        # If the stack is empty or the current bar is taller than the bar at the stack's top index
        if not stack or heights[index] >= heights[stack[-1]]:
            stack.append(index)
            index += 1
        else:
            # Pop the top index from the stack
            top_of_stack = stack.pop()
            # Calculate the area with heights[top_of_stack] as the smallest bar
            area = (heights[top_of_stack] *
                   ((index - stack[-1] - 1) if stack else index))
            # Update max_area if the calculated area is larger
            max_area = max(max_area, area)

    # Pop the remaining bars from the stack and calculate the area for each
    while stack:
        top_of_stack = stack.pop()
        area = (heights[top_of_stack] *
               ((index - stack[-1] - 1) if stack else index))
        max_area = max(max_area, area)

    return max_area

Complexity Analysis

The time complexity of this approach is O(n) because each bar is pushed and popped from the stack at most once. The space complexity is O(n) due to the stack used to store the indices.

Edge Cases

Potential edge cases include:

  • All bars have the same height.
  • Only one bar in the histogram.
  • Bars with height 0.

Each of these cases is handled by the algorithm as it iterates through all bars and calculates the area accordingly.

Testing

To test the solution comprehensively, consider the following test cases:

assert largestRectangleArea([2,1,5,6,2,3]) == 10
assert largestRectangleArea([2,4]) == 4
assert largestRectangleArea([0,0,0,0]) == 0
assert largestRectangleArea([1,1,1,1]) == 4
assert largestRectangleArea([6,2,5,4,5,1,6]) == 12

Thinking and Problem-Solving Tips

When approaching such problems, it is crucial to:

  • Understand the problem constraints and requirements.
  • Think about different approaches and their time complexities.
  • Use data structures like stacks to optimize the solution.
  • Practice similar problems to improve problem-solving skills.

Conclusion

In this blog post, we discussed the problem of finding the largest rectangle in a histogram. We explored a stack-based approach to solve the problem efficiently in O(n) time complexity. Understanding and solving such problems is essential for improving algorithmic thinking and problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources: