Algocademy Logo

Intersection of Two Linked Lists in O(m + n) Time Complexity using Python


Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:



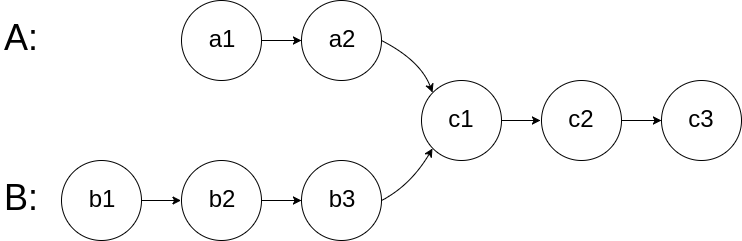
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

  • intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
  • listA - The first linked list.
  • listB - The second linked list.
  • skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
  • skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.

The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.

 

Example 1:



Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

Example 2:



Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:



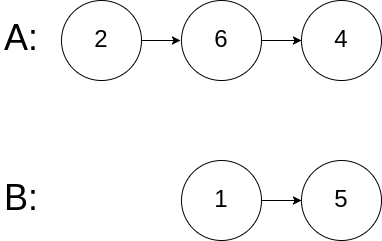
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

 

Constraints:

  • The number of nodes of listA is in the m.
  • The number of nodes of listB is in the n.
  • 1 <= m, n <= 3 * 104
  • 1 <= Node.val <= 105
  • 0 <= skipA < m
  • 0 <= skipB < n
  • intersectVal is 0 if listA and listB do not intersect.
  • intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

 

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

Understanding the Problem

The core challenge of this problem is to identify the node at which two singly linked lists intersect. This is a common problem in linked list manipulation and has applications in various fields such as network routing, version control systems, and more. A potential pitfall is assuming that the lists intersect at the same position from the start, which is not necessarily true.

Approach

To solve this problem, we can use the following approaches:

Naive Approach

The naive approach involves using two nested loops to compare each node of the first list with each node of the second list. This approach has a time complexity of O(m * n), which is not optimal for large lists.

Optimized Approach

We can optimize the solution by using two pointers. The idea is to traverse both lists and switch to the other list once the end is reached. This way, both pointers will traverse the same number of nodes and meet at the intersection point if there is one.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

  1. Initialize two pointers, pA and pB, to the heads of headA and headB respectively.
  2. Traverse the lists with the pointers. When a pointer reaches the end of a list, switch it to the head of the other list.
  3. If the lists intersect, the pointers will meet at the intersection node. If they do not intersect, both pointers will eventually be null.

Code Implementation

Here is the Python code for the optimized solution:

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

def getIntersectionNode(headA, headB):
    # Initialize two pointers
    pA, pB = headA, headB
    
    # Traverse the lists
    while pA != pB:
        # If pA reaches the end, switch to headB
        pA = pA.next if pA else headB
        # If pB reaches the end, switch to headA
        pB = pB.next if pB else headA
    
    # Either both pointers meet at the intersection node or both are null
    return pA

Complexity Analysis

The time complexity of this approach is O(m + n), where m and n are the lengths of the two linked lists. The space complexity is O(1) since we are using only two pointers.

Edge Cases

Potential edge cases include:

These cases are handled by the algorithm as it ensures that both pointers traverse the same number of nodes.

Testing

To test the solution comprehensively, consider the following test cases:

Using a testing framework like unittest in Python can help automate and validate these test cases.

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

Conclusion

In this blog post, we discussed the problem of finding the intersection of two linked lists. We explored a naive approach and an optimized approach using two pointers. The optimized solution runs in O(m + n) time and uses O(1) space. Understanding and solving such problems is crucial for improving algorithmic thinking and coding skills.

Additional Resources

For further reading and practice, consider the following resources: