Flatten Binary Tree in Python

Given the root of a binary tree, flatten the tree into a "linked list":

The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

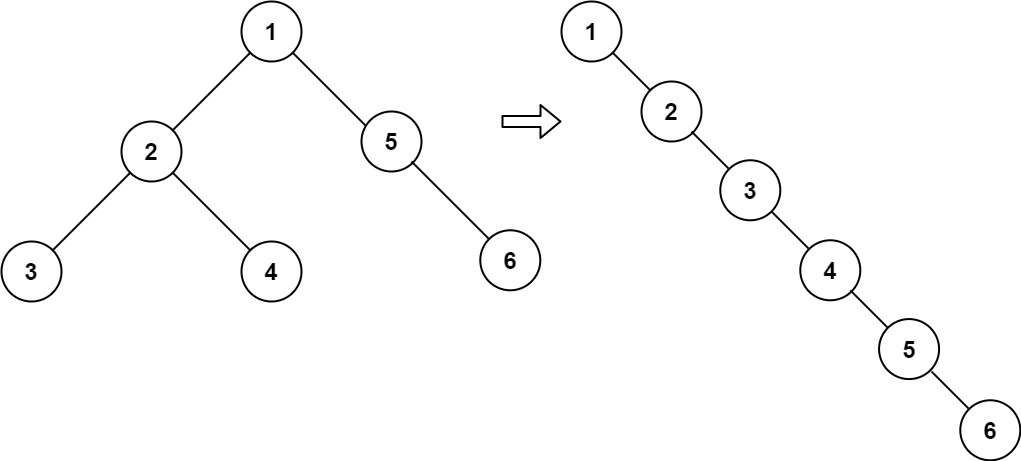
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

Understanding the Problem

The core challenge of this problem is to transform a binary tree into a linked list using the same TreeNode class. The transformation should follow a pre-order traversal, meaning we visit the root node first, then recursively visit the left subtree, and finally the right subtree. The left child pointer of each node should be set to null, and the right child pointer should point to the next node in the pre-order sequence.

This problem is significant in scenarios where we need to serialize a tree structure into a linear form for easier traversal or storage. A common pitfall is to forget to set the left child pointers to null or to not maintain the pre-order traversal order.

Approach

To solve this problem, we can consider the following approaches:

Naive Approach

A naive approach would be to perform a pre-order traversal of the tree, store the nodes in a list, and then re-link the nodes to form the desired linked list. However, this approach requires additional space to store the nodes, which is not optimal.

Optimized Approach

An optimized approach is to modify the tree in place during the traversal. We can use a recursive function to flatten the tree. The idea is to recursively flatten the left and right subtrees and then re-link the nodes accordingly.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

If the root is null, return immediately.
Recursively flatten the left subtree.
Recursively flatten the right subtree.
Store the right subtree in a temporary variable.
Move the left subtree to the right and set the left child to null.
Traverse to the end of the new right subtree and attach the previously stored right subtree.

Code Implementation

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def flatten(root):
    # Helper function to flatten the tree
    def flatten_tree(node):
        if not node:
            return None
        
        # Flatten the left and right subtrees
        left_tail = flatten_tree(node.left)
        right_tail = flatten_tree(node.right)
        
        # If there was a left subtree, we shuffle the connections
        if left_tail:
            left_tail.right = node.right
            node.right = node.left
            node.left = None
        
        # We need to return the "tail" of the flattened subtree
        return right_tail or left_tail or node
    
    flatten_tree(root)

Complexity Analysis

The time complexity of this approach is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.

Edge Cases

Consider the following edge cases:

An empty tree (root is null): The output should be an empty list.
A tree with a single node: The output should be the same single node.
A tree where all nodes have only left children or only right children: The algorithm should handle these cases correctly and produce a linear linked list.

Testing

To test the solution comprehensively, consider the following test cases:

def test_flatten():
    # Test case 1: Example 1
    root = TreeNode(1, TreeNode(2, TreeNode(3), TreeNode(4)), TreeNode(5, None, TreeNode(6)))
    flatten(root)
    assert root.val == 1
    assert root.right.val == 2
    assert root.right.right.val == 3
    assert root.right.right.right.val == 4
    assert root.right.right.right.right.val == 5
    assert root.right.right.right.right.right.val == 6

    # Test case 2: Example 2
    root = None
    flatten(root)
    assert root == None

    # Test case 3: Example 3
    root = TreeNode(0)
    flatten(root)
    assert root.val == 0
    assert root.right == None

    print("All test cases pass")

test_flatten()

Thinking and Problem-Solving Tips

When approaching such problems, it is essential to:

Understand the traversal order required (pre-order, in-order, post-order).
Consider whether the problem can be solved in place or requires additional space.
Break down the problem into smaller subproblems and solve them recursively.
Test the solution with various edge cases to ensure its robustness.

Conclusion

Flattening a binary tree into a linked list is a common problem that tests your understanding of tree traversal and in-place modifications. By following the optimized approach discussed, you can solve this problem efficiently with a time complexity of O(n). Practice and understanding of such problems are crucial for improving your problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources:

Flatten Binary Tree (Python, O(n) Time Complexity)