N Queens Problem in JavaScript (Time Complexity: O(N!))

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, and is represented as an array containing the column for each row of the matrix.

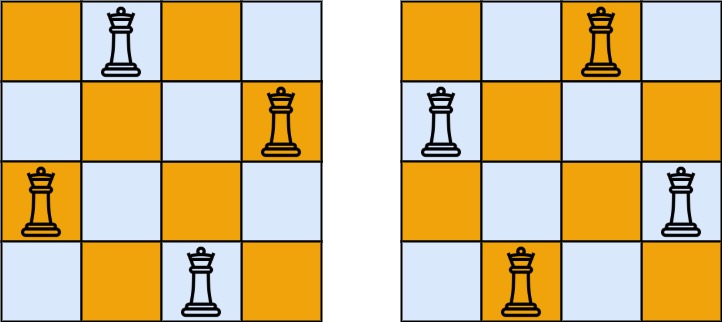
Example:

Input: n = 4
Output: [[1, 3, 0, 2], [2, 0, 3, 1]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Constraints:

1 <= n <= 9

Understanding the Problem

The core challenge of the n-queens problem is to place n queens on an n x n chessboard such that no two queens can attack each other. This means no two queens can be in the same row, column, or diagonal.

This problem is significant in the field of computer science and mathematics as it involves backtracking, a fundamental algorithmic technique. It also has applications in constraint satisfaction problems and combinatorial optimization.

Potential pitfalls include misunderstanding the constraints of the problem, such as ensuring no two queens share the same diagonal, which can be tricky to implement correctly.

Approach

To solve the n-queens problem, we can use a backtracking approach. The idea is to place queens one by one in different columns, starting from the leftmost column. When placing a queen, we check for clashes with already placed queens. If a clash is found, we backtrack and try the next column.

Here is a step-by-step approach:

Start in the leftmost column.
If all queens are placed, return the solution.
Try all rows in the current column. For each row, do the following:
- If the queen can be placed safely in this row, mark this cell and move to the next column.
- If placing the queen in the current row leads to a solution, return true.
- If placing the queen in the current row does not lead to a solution, unmark this cell (backtrack) and try the next row.
If all rows have been tried and none worked, return false to trigger backtracking.

Algorithm

Here is a detailed breakdown of the algorithm:

Create a helper function to check if a queen can be placed at a given position.
Create a recursive function to solve the problem using backtracking.
Use an array to store the positions of the queens.
Iterate through each column and try placing a queen in each row.
If a valid position is found, place the queen and move to the next column.
If placing the queen leads to a solution, add the solution to the result list.
If no valid position is found, backtrack and try the next row.

Code Implementation

/**
 * Solves the n-queens problem and returns all distinct solutions.
 * @param {number} n - The size of the chessboard.
 * @return {number[][]} - A list of solutions, each solution is an array of column indices.
 */
function solveNQueens(n) {
    const solutions = [];
    const board = new Array(n).fill(0).map(() => new Array(n).fill('.'));
    const cols = new Set();
    const diag1 = new Set();
    const diag2 = new Set();

    function backtrack(row) {
        if (row === n) {
            const solution = board.map(r => r.join(''));
            solutions.push(solution);
            return;
        }

        for (let col = 0; col < n; col++) {
            if (cols.has(col) || diag1.has(row - col) || diag2.has(row + col)) {
                continue;
            }

            board[row][col] = 'Q';
            cols.add(col);
            diag1.add(row - col);
            diag2.add(row + col);

            backtrack(row + 1);

            board[row][col] = '.';
            cols.delete(col);
            diag1.delete(row - col);
            diag2.delete(row + col);
        }
    }

    backtrack(0);
    return solutions;
}

// Example usage:
console.log(solveNQueens(4));

Complexity Analysis

The time complexity of the backtracking solution is O(N!), where N is the size of the chessboard. This is because we are trying every possible placement of queens and backtracking when necessary.

The space complexity is O(N) for the recursion stack and the sets used to track columns and diagonals.

Edge Cases

Some potential edge cases include:

n = 1: The solution is trivial as there is only one cell.
n = 2 or n = 3: There are no solutions for these values as it's impossible to place the queens without them attacking each other.

To handle these edge cases, we can add checks at the beginning of our function to return early for these values.

Testing

To test the solution comprehensively, we should include a variety of test cases:

Simple cases like n = 1, 2, 3.
Standard cases like n = 4, 5, 6.
Edge cases like n = 9 (the upper limit).

We can use console logs or a testing framework like Jest to automate the testing process.

Thinking and Problem-Solving Tips

When approaching problems like the n-queens puzzle, it's important to:

Break down the problem into smaller, manageable parts.
Use diagrams or visual aids to understand the problem better.
Think about edge cases and constraints early on.
Practice similar problems to improve your problem-solving skills.

Conclusion

The n-queens problem is a classic example of a backtracking problem. By understanding the constraints and using a systematic approach, we can find all possible solutions efficiently. This problem helps in developing a deeper understanding of backtracking and its applications in solving complex problems.

Additional Resources

For further reading and practice, consider the following resources: