Maximum Sum BST in Binary Tree: II - JavaScript Solution and Time Complexity Analysis

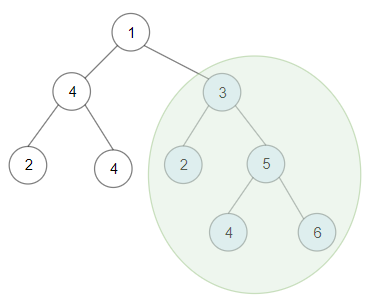
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

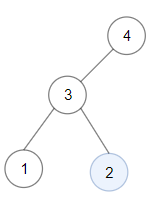
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Input: root = [2,1,3]
Output: 6

Input: root = [5,4,8,3,null,6,3]
Output: 7

Understanding the Problem

The core challenge of this problem is to identify the sub-trees within a given binary tree that are valid Binary Search Trees (BSTs) and then calculate the sum of their nodes. The goal is to find the maximum sum among all such BST sub-trees.

This problem is significant in various applications such as database indexing, memory management, and more, where efficient data retrieval and manipulation are crucial.

Potential pitfalls include incorrectly identifying BSTs and not handling edge cases like negative values or single-node trees.

Approach

To solve this problem, we need to traverse the tree and check each sub-tree to see if it is a valid BST. A naive approach would involve checking every possible sub-tree, but this would be highly inefficient.

Instead, we can use a post-order traversal (left-right-root) to gather information about each sub-tree and determine if it is a BST. This allows us to efficiently calculate the sum of nodes for valid BSTs and keep track of the maximum sum encountered.

Naive Solution

The naive solution involves checking every possible sub-tree to see if it is a BST and then calculating the sum of its nodes. This approach is not optimal due to its high time complexity.

Optimized Solution

The optimized solution uses a post-order traversal to gather information about each sub-tree. For each node, we check if its left and right sub-trees are BSTs and if the current node satisfies the BST properties. If it does, we calculate the sum of the current sub-tree and update the maximum sum if necessary.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

1. Perform a post-order traversal of the tree.
2. For each node, gather information about its left and right sub-trees (whether they are BSTs, their sums, and their min/max values).
3. Check if the current node forms a valid BST with its left and right sub-trees.
4. If it does, calculate the sum of the current sub-tree and update the maximum sum if necessary.
5. Return the maximum sum encountered.

Code Implementation

Below is the JavaScript implementation of the optimized solution:

// Definition for a binary tree node.
function TreeNode(val, left, right) {
    this.val = (val===undefined ? 0 : val)
    this.left = (left===undefined ? null : left)
    this.right = (right===undefined ? null : right)
}

function maxSumBST(root) {
    let maxSum = 0;

    function postOrder(node) {
        if (!node) return [true, 0, Infinity, -Infinity];

        const [leftIsBST, leftSum, leftMin, leftMax] = postOrder(node.left);
        const [rightIsBST, rightSum, rightMin, rightMax] = postOrder(node.right);

        if (leftIsBST && rightIsBST && node.val > leftMax && node.val < rightMin) {
            const sum = node.val + leftSum + rightSum;
            maxSum = Math.max(maxSum, sum);
            return [true, sum, Math.min(node.val, leftMin), Math.max(node.val, rightMax)];
        } else {
            return [false, 0, 0, 0];
        }
    }

    postOrder(root);
    return maxSum;
}

// Example usage:
const root = new TreeNode(1, 
    new TreeNode(4, 
        new TreeNode(2), 
        new TreeNode(4)
    ), 
    new TreeNode(3, 
        new TreeNode(2), 
        new TreeNode(5, 
            new TreeNode(4), 
            new TreeNode(6)
        )
    )
);

console.log(maxSumBST(root)); // Output: 20

Complexity Analysis

The time complexity of the optimized solution is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once during the post-order traversal.

The space complexity is O(h), where h is the height of the tree. This is due to the recursive call stack used during the traversal.

Edge Cases

Potential edge cases include:

• All nodes have negative values: The algorithm should return 0 as the maximum sum.
• Single-node trees: The algorithm should correctly identify the single node as a valid BST and return its value.
• Empty trees: The algorithm should return 0.

Testing for these edge cases ensures the robustness of the solution.

Testing

To test the solution comprehensively, consider the following test cases:

• Simple trees with a few nodes.
• Large trees with thousands of nodes.
• Trees with all negative values.
• Trees with mixed positive and negative values.

Using a testing framework like Jest can help automate and manage these tests effectively.

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

• Break down the problem into smaller sub-problems.
• Use tree traversal techniques to gather information about sub-trees.
• Think about the properties of BSTs and how they can be leveraged to optimize the solution.
• Practice solving similar problems to improve problem-solving skills.

Conclusion

In this blog post, we discussed the problem of finding the maximum sum of keys in any sub-tree of a binary tree that is also a BST. We explored a naive solution and an optimized solution using post-order traversal. We also analyzed the complexity, considered edge cases, and provided testing strategies.

Understanding and solving such problems is crucial for developing efficient algorithms and improving problem-solving skills. Practice and exploration of similar problems can further enhance these skills.

Additional Resources

For further reading and practice, consider the following resources:

• LeetCode Problem
• GeeksforGeeks: Binary Search Tree
• Coursera: Data Structures and Optimizing Performance
• HackerRank: 10 Days of JavaScript