Maximum Sum BST in Binary Tree (JavaScript, Time Complexity Analysis)

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

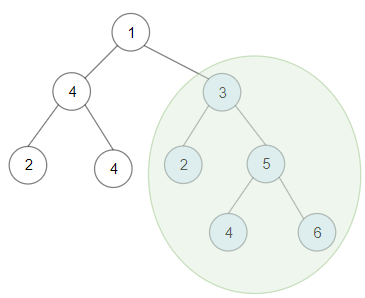
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

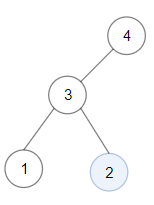
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

Constraints:

Each tree has at most 40000 nodes..
Each node's value is between [-4 * 10^4 , 4 * 10^4].

Understanding the Problem

The core challenge of this problem is to identify the largest sum of keys in any subtree that is a valid Binary Search Tree (BST). A BST is defined by the property that for any node, all nodes in its left subtree have keys less than the node's key, and all nodes in its right subtree have keys greater than the node's key. This problem has significant applications in data structures and algorithms, particularly in scenarios where hierarchical data needs to be optimized or analyzed.

Approach

To solve this problem, we need to traverse the tree and evaluate each subtree to determine if it is a BST and calculate its sum. A naive approach would involve checking each subtree individually, but this would be highly inefficient. Instead, we can use a post-order traversal to evaluate each node's subtrees and determine if they form a BST, while simultaneously calculating the sum of their keys.

Naive Solution

The naive solution involves checking each subtree to see if it is a BST and then calculating its sum. This approach is not optimal because it involves redundant checks and calculations, leading to a high time complexity.

Optimized Solution

An optimized solution involves using a post-order traversal to evaluate each node's subtrees. During the traversal, we can keep track of the minimum and maximum values in the subtrees, as well as their sums. This allows us to determine if the current subtree is a BST and calculate its sum efficiently.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

Perform a post-order traversal of the tree.
For each node, evaluate its left and right subtrees.
Keep track of the minimum and maximum values in the subtrees, as well as their sums.
If the current node's value is greater than the maximum value in the left subtree and less than the minimum value in the right subtree, the current subtree is a BST.
Calculate the sum of the current subtree and update the maximum sum if it is greater than the previous maximum sum.

Code Implementation

// Definition for a binary tree node.
function TreeNode(val, left, right) {
    this.val = (val===undefined ? 0 : val)
    this.left = (left===undefined ? null : left)
    this.right = (right===undefined ? null : right)
}

function maxSumBST(root) {
    let maxSum = 0;

    function postOrder(node) {
        if (!node) {
            return { isBST: true, sum: 0, min: Infinity, max: -Infinity };
        }

        const left = postOrder(node.left);
        const right = postOrder(node.right);

        if (left.isBST && right.isBST && node.val > left.max && node.val < right.min) {
            const sum = node.val + left.sum + right.sum;
            maxSum = Math.max(maxSum, sum);
            return {
                isBST: true,
                sum: sum,
                min: Math.min(node.val, left.min),
                max: Math.max(node.val, right.max)
            };
        } else {
            return { isBST: false, sum: 0, min: -Infinity, max: Infinity };
        }
    }

    postOrder(root);
    return maxSum;
}

// Example usage:
const root = new TreeNode(1, 
    new TreeNode(4, new TreeNode(2), new TreeNode(4)), 
    new TreeNode(3, new TreeNode(2), new TreeNode(5, new TreeNode(4), new TreeNode(6)))
);
console.log(maxSumBST(root)); // Output: 20

Complexity Analysis

The time complexity of the optimized solution is O(n), where n is the number of nodes in the tree. This is because we perform a single post-order traversal of the tree. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.

Edge Cases

Potential edge cases include:

Empty tree: The function should return 0.
All negative values: The function should return 0 if no valid BST can be formed.
Single node tree: The function should return the value of the single node.

These edge cases can be tested by providing appropriate input trees and verifying the output.

Testing

To test the solution comprehensively, we can use a variety of test cases, including simple and complex trees, trees with negative values, and edge cases. Here are some example test cases:

// Test case 1: Simple tree
const root1 = new TreeNode(2, new TreeNode(1), new TreeNode(3));
console.log(maxSumBST(root1)); // Output: 6

// Test case 2: Tree with negative values
const root2 = new TreeNode(-4, new TreeNode(-2), new TreeNode(-5));
console.log(maxSumBST(root2)); // Output: 0

// Test case 3: Complex tree
const root3 = new TreeNode(5, 
    new TreeNode(4, new TreeNode(3)), 
    new TreeNode(8, new TreeNode(6), new TreeNode(3))
);
console.log(maxSumBST(root3)); // Output: 7

Thinking and Problem-Solving Tips

When approaching such problems, it is important to:

Understand the problem requirements and constraints thoroughly.
Break down the problem into smaller sub-problems and solve them incrementally.
Consider edge cases and test your solution comprehensively.
Practice solving similar problems to improve problem-solving skills.

Conclusion

In this blog post, we discussed the problem of finding the maximum sum of keys in any subtree of a binary tree that is also a BST. We explored a naive solution and an optimized solution using post-order traversal. We also provided a detailed code implementation, complexity analysis, and testing strategies. Understanding and solving such problems is crucial for improving algorithmic thinking and problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources: