Linked List Cycle Detection in JavaScript (Time Complexity: O(n), Space Complexity: O(1))

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

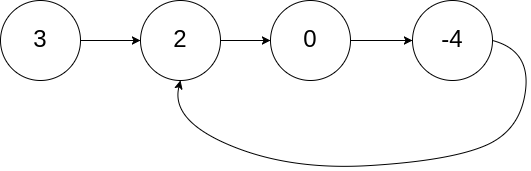
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

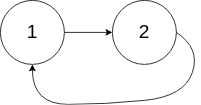
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10⁴].
-10⁵ <= Node.val <= 10⁵
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Understanding the Problem

The core challenge of this problem is to detect if a linked list contains a cycle. A cycle occurs when a node's next pointer points back to a previous node, creating a loop. This problem is significant in various applications, such as detecting infinite loops in programs or ensuring data structures' integrity.

Potential pitfalls include misunderstanding the problem's constraints or failing to handle edge cases, such as an empty list or a single node without a cycle.

Approach

To solve this problem, we can use two primary approaches:

Naive Approach: Use a hash set to track visited nodes. If we encounter a node that is already in the set, a cycle exists. This approach has a time complexity of O(n) and a space complexity of O(n).
Optimized Approach: Use Floyd's Tortoise and Hare algorithm, which uses two pointers moving at different speeds. If there is a cycle, the fast pointer (hare) will eventually meet the slow pointer (tortoise). This approach has a time complexity of O(n) and a space complexity of O(1).

Naive Approach

In the naive approach, we use a hash set to keep track of visited nodes. As we traverse the linked list, we check if the current node is already in the set. If it is, we return true, indicating a cycle. If we reach the end of the list without finding a cycle, we return false.

Optimized Approach: Floyd's Tortoise and Hare Algorithm

In this approach, we use two pointers, slow and fast. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time. If there is a cycle, the fast pointer will eventually meet the slow pointer. If the fast pointer reaches the end of the list, there is no cycle.

Algorithm

Naive Approach

// Naive approach using a hash set
var hasCycle = function(head) {
    let visited = new Set();
    let current = head;
    
    while (current !== null) {
        // If the current node is already in the set, we have a cycle
        if (visited.has(current)) {
            return true;
        }
        // Add the current node to the set
        visited.add(current);
        // Move to the next node
        current = current.next;
    }
    
    // If we reach here, there is no cycle
    return false;
};

Optimized Approach: Floyd's Tortoise and Hare Algorithm

// Optimized approach using Floyd's Tortoise and Hare algorithm
var hasCycle = function(head) {
    if (head === null || head.next === null) {
        return false;
    }
    
    let slow = head;
    let fast = head.next;
    
    while (slow !== fast) {
        if (fast === null || fast.next === null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    
    return true;
};

Complexity Analysis

Naive Approach:

Time Complexity: O(n) - We traverse the entire list once.
Space Complexity: O(n) - We use a hash set to store visited nodes.

Optimized Approach:

Time Complexity: O(n) - In the worst case, we traverse the entire list once.
Space Complexity: O(1) - We use only two pointers, regardless of the list size.

Edge Cases

Consider the following edge cases:

An empty list (head is null) - The function should return false.
A single node without a cycle - The function should return false.
A single node with a cycle (node points to itself) - The function should return true.

Testing

To test the solution comprehensively, consider the following test cases:

// Test case 1: List with a cycle
let head1 = { val: 3, next: null };
let node2 = { val: 2, next: null };
let node3 = { val: 0, next: null };
let node4 = { val: -4, next: null };
head1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node2; // Creates a cycle
console.log(hasCycle(head1)); // Output: true

// Test case 2: List without a cycle
let head2 = { val: 1, next: null };
let node5 = { val: 2, next: null };
head2.next = node5;
console.log(hasCycle(head2)); // Output: false

// Test case 3: Empty list
console.log(hasCycle(null)); // Output: false

// Test case 4: Single node without a cycle
let head3 = { val: 1, next: null };
console.log(hasCycle(head3)); // Output: false

// Test case 5: Single node with a cycle
let head4 = { val: 1, next: null };
head4.next = head4; // Creates a cycle
console.log(hasCycle(head4)); // Output: true

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

Understand the problem constraints and edge cases.
Start with a simple, naive solution to understand the problem better.
Think about optimizing the solution in terms of time and space complexity.
Practice solving similar problems to improve problem-solving skills.

Conclusion

Detecting a cycle in a linked list is a common problem with practical applications. Understanding and implementing both the naive and optimized approaches helps in grasping the underlying concepts. Practice and familiarity with such problems will improve your problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources: