Largest Rectangle in Histogram - JavaScript Solution with O(n) Time Complexity

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

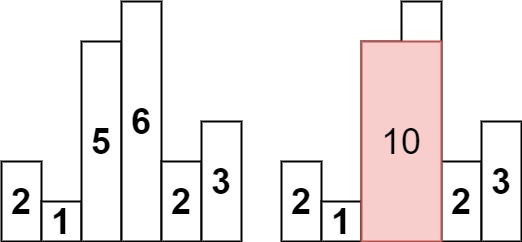
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

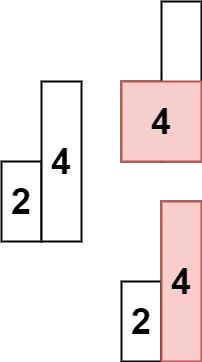
Input: heights = [2,4]
Output: 4

Constraints:

1 <= heights.length <= 10⁵
0 <= heights[i] <= 10⁴

Understanding the Problem

The core challenge of this problem is to find the largest rectangular area that can be formed within the histogram. This problem is significant in various applications such as image processing, data visualization, and computational geometry. A common pitfall is to attempt a brute-force solution, which is not efficient for large inputs.

Approach

To solve this problem efficiently, we can use a stack-based approach. The idea is to use a stack to keep track of the indices of the histogram bars. This allows us to efficiently calculate the largest rectangle for each bar by considering it as the smallest (or minimum height) bar in the rectangle.

Naive Solution

A naive solution would involve checking every possible rectangle by iterating through all pairs of bars. This approach has a time complexity of O(n^2) and is not feasible for large inputs.

Optimized Solution

The optimized solution uses a stack to keep track of the indices of the bars. The stack helps in maintaining the bars in increasing order of their heights. When we encounter a bar that is shorter than the bar at the top of the stack, we calculate the area of the rectangle with the height of the bar at the top of the stack as the smallest (or minimum height) bar. This approach ensures that each bar is pushed and popped from the stack only once, resulting in a time complexity of O(n).

Algorithm

Here is a step-by-step breakdown of the stack-based algorithm:

Initialize an empty stack and a variable to store the maximum area.
Iterate through each bar in the histogram.
For each bar, if the stack is empty or the current bar is taller than the bar at the top of the stack, push its index onto the stack.
If the current bar is shorter than the bar at the top of the stack, pop the stack and calculate the area of the rectangle with the popped bar as the smallest bar. Update the maximum area if the calculated area is larger.
After iterating through all bars, pop the remaining bars in the stack and calculate the area for each.

Code Implementation

/**
 * @param {number[]} heights
 * @return {number}
 */
function largestRectangleArea(heights) {
    // Initialize an empty stack and maxArea variable
    let stack = [];
    let maxArea = 0;
    let index = 0;

    // Iterate through all bars in the histogram
    while (index < heights.length) {
        // If the stack is empty or the current bar is taller than the bar at the top of the stack
        if (stack.length === 0 || heights[index] >= heights[stack[stack.length - 1]]) {
            stack.push(index);
            index++;
        } else {
            // Pop the top of the stack and calculate the area
            let topOfStack = stack.pop();
            let area = heights[topOfStack] * (stack.length === 0 ? index : index - stack[stack.length - 1] - 1);
            maxArea = Math.max(maxArea, area);
        }
    }

    // Pop the remaining bars in the stack and calculate the area
    while (stack.length > 0) {
        let topOfStack = stack.pop();
        let area = heights[topOfStack] * (stack.length === 0 ? index : index - stack[stack.length - 1] - 1);
        maxArea = Math.max(maxArea, area);
    }

    return maxArea;
}

Complexity Analysis

The time complexity of the optimized solution is O(n) because each bar is pushed and popped from the stack only once. The space complexity is O(n) due to the stack used to store the indices of the bars.

Edge Cases

Potential edge cases include:

All bars have the same height.
Bars with height 0.
Single bar in the histogram.

Each of these cases is handled by the algorithm as it iterates through all bars and calculates the area accordingly.

Testing

To test the solution comprehensively, consider the following test cases:

console.log(largestRectangleArea([2,1,5,6,2,3])); // Output: 10
console.log(largestRectangleArea([2,4])); // Output: 4
console.log(largestRectangleArea([0,0,0,0])); // Output: 0
console.log(largestRectangleArea([1,1,1,1])); // Output: 4
console.log(largestRectangleArea([1])); // Output: 1

Thinking and Problem-Solving Tips

When approaching such problems, it is essential to:

Understand the problem requirements and constraints thoroughly.
Consider edge cases and how the algorithm handles them.
Break down the problem into smaller, manageable parts.
Use data structures like stacks to optimize the solution.

Practice solving similar problems and study different algorithms to improve problem-solving skills.

Conclusion

In this blog post, we discussed the problem of finding the largest rectangle in a histogram. We explored a stack-based approach to solve the problem efficiently with a time complexity of O(n). Understanding and solving such problems is crucial for improving algorithmic thinking and problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources: