Flatten Binary Tree in JavaScript

Given the root of a binary tree, flatten the tree into a "linked list":

The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

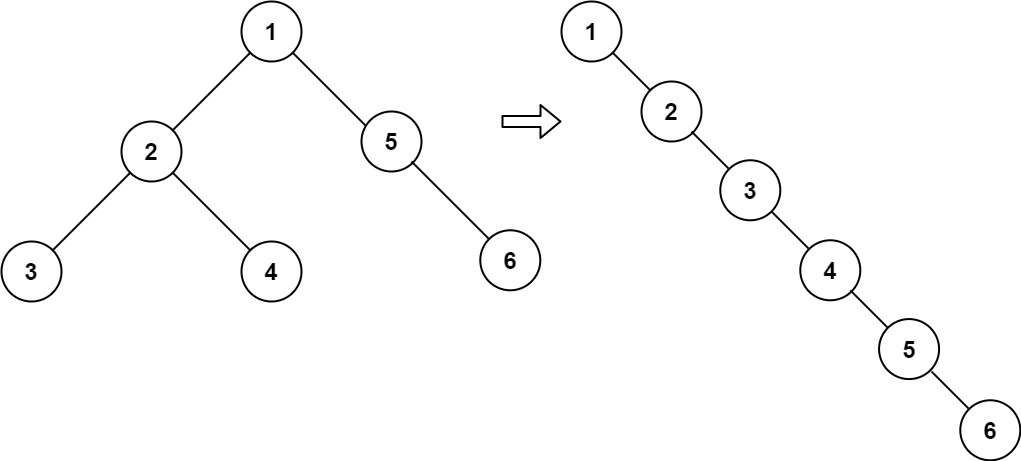
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

Understanding the Problem

The core challenge of this problem is to transform a binary tree into a linked list using the same TreeNode class. The linked list should follow the pre-order traversal of the tree. This means we need to visit the root node first, then recursively visit the left subtree, and finally the right subtree.

This problem is significant in scenarios where tree structures need to be linearized for easier traversal or storage. Common applications include serialization of trees and simplifying tree-based algorithms.

Potential pitfalls include not maintaining the pre-order traversal order and not correctly setting the left child pointers to null.

Approach

To solve this problem, we can use a recursive approach to perform a pre-order traversal and modify the tree in place. Here’s a step-by-step breakdown:

Naive Solution

A naive solution would involve performing a pre-order traversal, storing the nodes in a list, and then re-linking them. However, this approach uses extra space for the list, which is not optimal.

Optimized Solution

An optimized solution involves modifying the tree in place during the traversal. We can use a recursive function to flatten the tree:

Recursively flatten the left and right subtrees.
Store the right subtree and move the left subtree to the right.
Attach the originally right subtree to the end of the new right subtree.

Algorithm

Here’s a step-by-step breakdown of the optimized algorithm:

If the root is null, return immediately.
Recursively flatten the left subtree.
Recursively flatten the right subtree.
Store the right subtree in a temporary variable.
Move the left subtree to the right and set the left child to null.
Find the end of the new right subtree and attach the originally right subtree.

Code Implementation

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */

/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
    if (!root) return;

    // Flatten the left and right subtrees
    flatten(root.left);
    flatten(root.right);

    // Store the right subtree
    let tempRight = root.right;

    // Move the left subtree to the right
    root.right = root.left;
    root.left = null;

    // Find the end of the new right subtree
    let current = root;
    while (current.right) {
        current = current.right;
    }

    // Attach the originally right subtree
    current.right = tempRight;
};

Complexity Analysis

The time complexity of this approach is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.

Edge Cases

Consider the following edge cases:

An empty tree (root is null) - The function should handle this gracefully and return without modifying anything.
A tree with only one node - The function should return the same single node as the linked list.

Testing for these edge cases ensures the robustness of the solution.

Testing

To test the solution comprehensively, consider the following test cases:

A balanced binary tree.
A skewed tree (all nodes have only left or only right children).
A tree with varying subtree sizes.

Using a testing framework like Jest can help automate and validate these test cases.

Thinking and Problem-Solving Tips

When approaching such problems, it’s essential to:

Understand the traversal order required (pre-order in this case).
Think about how to modify the tree in place to avoid extra space usage.
Break down the problem into smaller subproblems and solve them recursively.

Practicing similar problems and studying tree traversal algorithms can significantly improve problem-solving skills.

Conclusion

Flattening a binary tree into a linked list in pre-order traversal order is a common problem that tests understanding of tree traversal and in-place modification. By following the optimized approach discussed, we can achieve an efficient solution with O(n) time complexity.

Understanding and solving such problems is crucial for mastering tree-based algorithms and improving overall problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources:

Flatten Binary Tree (JavaScript, O(n) Time Complexity) /homework