Binary Tree Diameter in JavaScript (Time Complexity: O(n))

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

 

Example 1:

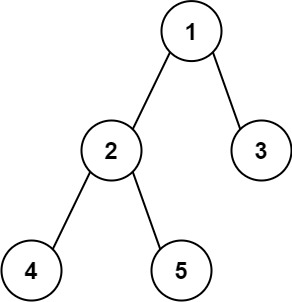
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -100 <= Node.val <= 100

Understanding the Problem

The core challenge of this problem is to find the longest path between any two nodes in a binary tree. This path does not necessarily have to pass through the root. The significance of this problem lies in its applications in network design, biology (e.g., finding the longest path in phylogenetic trees), and various other fields where tree structures are used.

Potential pitfalls include misunderstanding the definition of the diameter (it is the number of edges, not nodes) and not considering paths that do not pass through the root.

Approach

To solve this problem, we need to think about how to traverse the tree and calculate the longest path. A naive solution might involve checking all possible paths between nodes, but this would be highly inefficient.

Instead, we can use a depth-first search (DFS) approach to calculate the height of each subtree and use this information to determine the diameter. The height of a node is the number of edges on the longest path from the node to a leaf. The diameter can be found by considering the longest path that passes through each node.

Naive Solution

The naive solution involves calculating the path length between all pairs of nodes, which is not optimal due to its high time complexity.

Optimized Solution

An optimized solution involves a single DFS traversal of the tree. During this traversal, we calculate the height of each node and update the diameter based on the sum of the heights of the left and right subtrees.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

1. Define a helper function to calculate the height of a node.
2. During the height calculation, update the diameter based on the sum of the heights of the left and right subtrees.
3. Return the diameter after the DFS traversal is complete.

Code Implementation

// Definition for a binary tree node.
function TreeNode(val, left, right) {
    this.val = (val===undefined ? 0 : val);
    this.left = (left===undefined ? null : left);
    this.right = (right===undefined ? null : right);
}

var diameterOfBinaryTree = function(root) {
    let diameter = 0;

    // Helper function to calculate height
    function height(node) {
        if (node === null) return 0;

        // Recursively find the height of left and right subtrees
        let leftHeight = height(node.left);
        let rightHeight = height(node.right);

        // Update the diameter if the path through the current node is longer
        diameter = Math.max(diameter, leftHeight + rightHeight);

        // Return the height of the current node
        return Math.max(leftHeight, rightHeight) + 1;
    }

    // Start the DFS traversal from the root
    height(root);

    return diameter;
};

Complexity Analysis

The time complexity of this approach is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once during the DFS traversal. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.

Edge Cases

Potential edge cases include:

• A tree with only one node (the diameter is 0).
• A tree where all nodes are on one side (e.g., a linked list).

These cases are handled by the algorithm as it correctly calculates the height and updates the diameter accordingly.

Testing

To test the solution comprehensively, consider the following test cases:

• A balanced tree with multiple levels.
• A tree with only left or right children.
• A tree with a single node.

Use a testing framework like Jest or Mocha to automate the testing process.

Thinking and Problem-Solving Tips

When approaching such problems, it is essential to:

• Understand the problem definition and constraints thoroughly.
• Break down the problem into smaller subproblems.
• Consider different approaches and their trade-offs.
• Practice similar problems to improve problem-solving skills.

Conclusion

In this blog post, we discussed how to find the diameter of a binary tree using an optimized DFS approach. We covered the problem definition, approach, algorithm, code implementation, complexity analysis, edge cases, and testing. Understanding and solving such problems is crucial for improving algorithmic thinking and coding skills.

Additional Resources

For further reading and practice, consider the following resources:

• LeetCode Problem
• GeeksforGeeks Article
• Coursera Course on Data Structures