Add Two Numbers in JavaScript (Time Complexity: O(max(m, n)))

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Example 1:

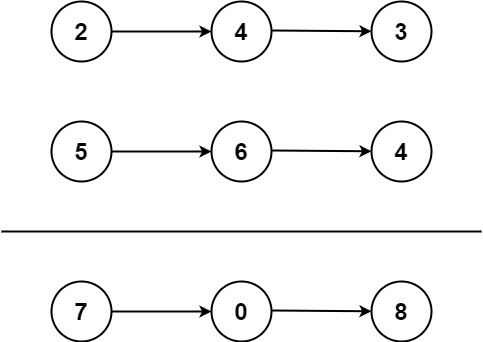
Input: list1 = [2, 4, 3], list2 = [5, 6, 4]
Output: [7, 0, 8]
Explanation: 342 + 465 = 807

Example 2:

Input: list1 = [9,9,9,9,9,9,9], list2 = [9,9,9,9]
Output: [8,9,9,9,0,0,0,1]
Explanation: 9999999 + 9999 = 10009998

Understanding the Problem

The core challenge of this problem is to handle the addition of two numbers represented as linked lists, where each node contains a single digit and the digits are stored in reverse order. This means the least significant digit comes first. The significance of this problem lies in its application to scenarios where numbers are too large to be handled by standard data types, and thus, are represented as linked lists.

Potential pitfalls include handling the carry-over during addition and ensuring that the resulting linked list correctly represents the sum in reverse order.

Approach

To solve this problem, we can use a straightforward approach by iterating through both linked lists simultaneously, adding corresponding digits along with any carry from the previous addition. If one list is shorter, we continue with the longer list while considering the carry.

Initial naive solution might involve converting the linked lists to integers, adding them, and then converting the result back to a linked list. However, this is not optimal due to potential overflow issues and inefficiency with very large numbers.

Optimized solution involves directly manipulating the linked lists without converting them to integers. This approach is more efficient and avoids overflow issues.

Algorithm

1. Initialize a dummy node to act as the head of the result linked list.

2. Initialize a current node pointing to the dummy node and a carry variable set to 0.

3. Iterate through both linked lists until both are exhausted and there is no carry:

Add the values of the current nodes of both lists (if they exist) along with the carry.
Update the carry for the next iteration.
Create a new node with the digit value of the current sum and attach it to the current node.
Move the current node to the next node.
Move to the next nodes in both linked lists (if they exist).

4. Return the next node of the dummy node as the head of the result linked list.

Code Implementation

// Definition for singly-linked list.
function ListNode(val, next = null) {
    this.val = val;
    this.next = next;
}

function addTwoNumbers(l1, l2) {
    // Initialize a dummy node to form the result list
    let dummy = new ListNode(0);
    let current = dummy;
    let carry = 0;

    // Iterate through both lists until both are exhausted and there is no carry
    while (l1 !== null || l2 !== null || carry !== 0) {
        // Get the values of the current nodes, if they exist
        let val1 = l1 !== null ? l1.val : 0;
        let val2 = l2 !== null ? l2.val : 0;

        // Calculate the sum and update the carry
        let sum = val1 + val2 + carry;
        carry = Math.floor(sum / 10);
        let digit = sum % 10;

        // Create a new node with the digit and attach it to the current node
        current.next = new ListNode(digit);
        current = current.next;

        // Move to the next nodes in both lists, if they exist
        if (l1 !== null) l1 = l1.next;
        if (l2 !== null) l2 = l2.next;
    }

    // Return the next node of the dummy node as the head of the result list
    return dummy.next;
}

Complexity Analysis

The time complexity of this approach is O(max(m, n)), where m and n are the lengths of the two linked lists. This is because we iterate through both lists simultaneously. The space complexity is also O(max(m, n)) due to the space required for the result linked list.

Edge Cases

Potential edge cases include:

One list is significantly longer than the other.
All nodes in both lists result in a carry.
One or both lists are empty (though the problem states they are non-empty).

Each of these cases is handled by the algorithm as it iterates through both lists and manages the carry appropriately.

Testing

To test the solution comprehensively, consider the following test cases:

Simple cases with no carry: [2, 4, 3] + [5, 6, 4]
Cases with carry: [9, 9, 9] + [1]
Different lengths: [1, 8] + [0]
All nodes result in carry: [9, 9, 9, 9, 9, 9, 9] + [9, 9, 9, 9]

Use a testing framework like Jest or Mocha to automate these tests and ensure the correctness of the solution.

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

Break down the problem into smaller, manageable parts.
Think about edge cases and how to handle them.
Write pseudocode to outline your approach before coding.
Test your solution with a variety of test cases.

To improve problem-solving skills, practice similar problems, study algorithms, and participate in coding challenges.

Conclusion

In this blog post, we discussed how to add two numbers represented as linked lists in JavaScript. We covered the problem definition, approach, algorithm, code implementation, complexity analysis, edge cases, and testing. Understanding and solving such problems is crucial for developing strong problem-solving skills and preparing for technical interviews.

Additional Resources

For further reading and practice, consider the following resources: