Flatten Binary Tree in Java

Given the root of a binary tree, flatten the tree into a "linked list":

The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

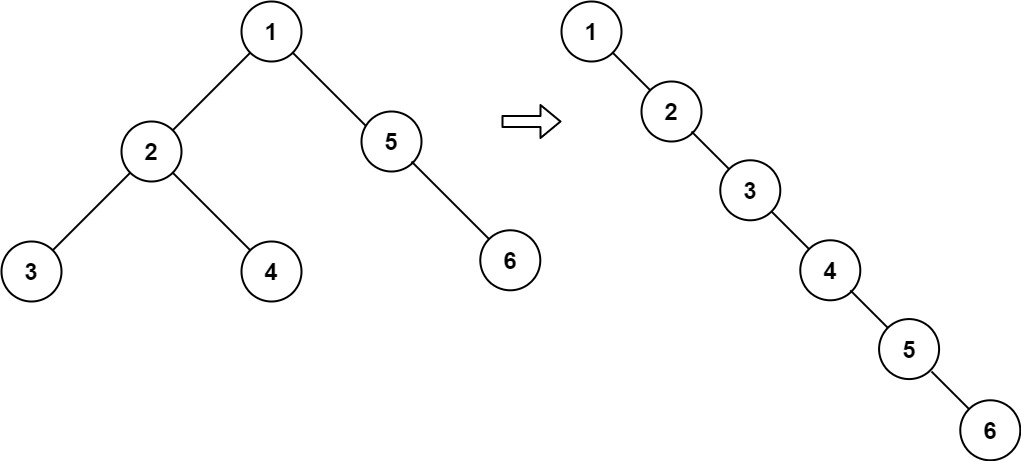
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

Understanding the Problem

The core challenge of this problem is to transform a binary tree into a linked list using the same TreeNode class. The transformation should follow a pre-order traversal, meaning we visit the root node first, then recursively visit the left subtree, and finally the right subtree. This problem is significant in scenarios where we need to serialize a tree structure into a linear form for easier traversal or storage.

Potential pitfalls include not maintaining the pre-order traversal order and not correctly setting the left child pointers to null.

Approach

To solve this problem, we can use a recursive approach to perform a pre-order traversal and modify the tree in place. Here are the steps:

Define a helper function that will recursively flatten the tree.
For each node, recursively flatten the left and right subtrees.
Store the right subtree and move the left subtree to the right.
Traverse to the end of the new right subtree and attach the previously stored right subtree.

We can also use an iterative approach with a stack to simulate the pre-order traversal and modify the tree accordingly.

Algorithm

Here is a step-by-step breakdown of the recursive algorithm:

If the root is null, return immediately.
Recursively flatten the left subtree.
Recursively flatten the right subtree.
Store the right subtree in a temporary variable.
Move the left subtree to the right and set the left child to null.
Traverse to the end of the new right subtree.
Attach the previously stored right subtree to the end of the new right subtree.

Code Implementation

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public void flatten(TreeNode root) {
        if (root == null) return;
        
        // Flatten the left and right subtrees
        flatten(root.left);
        flatten(root.right);
        
        // Store the right subtree
        TreeNode tempRight = root.right;
        
        // Move the left subtree to the right
        root.right = root.left;
        root.left = null;
        
        // Traverse to the end of the new right subtree
        TreeNode current = root;
        while (current.right != null) {
            current = current.right;
        }
        
        // Attach the previously stored right subtree
        current.right = tempRight;
    }
}

Complexity Analysis

The time complexity of this approach is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.

Edge Cases

Potential edge cases include:

An empty tree (root is null).
A tree with only one node.
A tree where all nodes are either to the left or right.

Each of these cases is handled by the algorithm as it checks for null nodes and processes each node individually.

Testing

To test the solution comprehensively, consider the following test cases:

An empty tree: root = []
A single node tree: root = [0]
A balanced tree: root = [1,2,5,3,4,null,6]
A left-skewed tree: root = [1,2,null,3,null,4]
A right-skewed tree: root = [1,null,2,null,3,null,4]

Use a testing framework like JUnit to automate these tests and ensure the correctness of the solution.

Thinking and Problem-Solving Tips

When approaching such problems, consider the following tips:

Understand the traversal order required (pre-order, in-order, post-order).
Think about how to modify the tree in place without using extra space.
Break down the problem into smaller subproblems and solve them recursively.
Practice similar problems to improve your understanding and skills.

Conclusion

Flattening a binary tree into a linked list is a common problem that tests your understanding of tree traversal and in-place modification. By following the recursive approach outlined above, you can efficiently solve this problem with a time complexity of O(n). Practice and explore further to strengthen your problem-solving skills.

Additional Resources

For further reading and practice, consider the following resources:

Flatten Binary Tree (Java, Time Complexity: O(n)) /homework