Flatten Binary Tree in C++

Given the root of a binary tree, flatten the tree into a "linked list":

The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

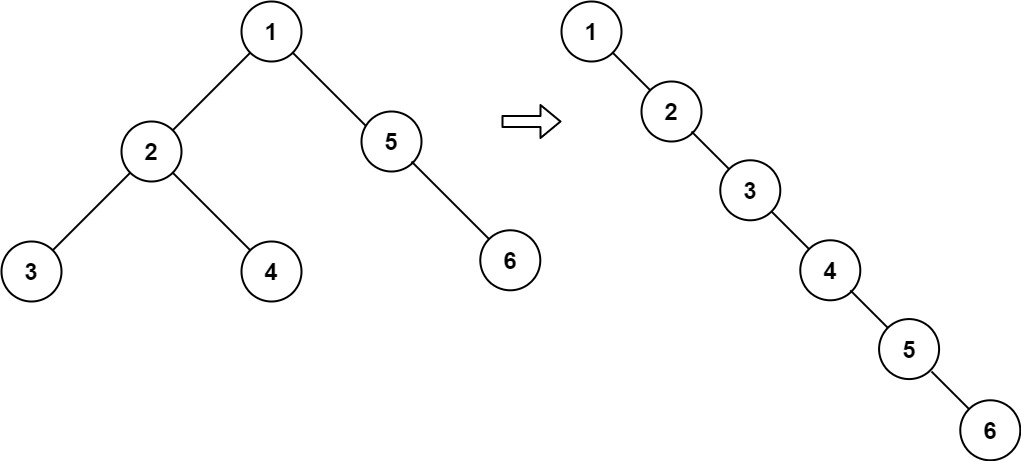
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

Understanding the Problem

The core challenge of this problem is to transform a binary tree into a linked list using the same TreeNode class. The transformation should follow a pre-order traversal, meaning we visit the root node first, then recursively visit the left subtree, and finally the right subtree. This problem is significant in scenarios where tree structures need to be linearized for easier traversal or storage.

Approach

To solve this problem, we can consider multiple approaches:

Naive Approach

A naive approach would involve performing a pre-order traversal of the tree and storing the nodes in a list. Then, we can iterate through the list to reassign the right pointers to form the linked list. However, this approach requires additional space for storing the nodes, making it less optimal.

Optimized Approach

An optimized approach involves modifying the tree in place without using extra space. We can achieve this by recursively flattening the left and right subtrees and then reassigning the pointers to form the linked list. This approach ensures that we only use O(1) extra space.

Algorithm

Here is a step-by-step breakdown of the optimized algorithm:

Recursively flatten the left and right subtrees.
Store the right subtree in a temporary variable.
Move the left subtree to the right and set the left pointer to null.
Traverse to the end of the new right subtree and attach the original right subtree.

Code Implementation


// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    void flatten(TreeNode* root) {
        if (!root) return;
        
        // Recursively flatten the left and right subtrees
        flatten(root->left);
        flatten(root->right);
        
        // Store the right subtree in a temporary variable
        TreeNode* tempRight = root->right;
        
        // Move the left subtree to the right and set the left pointer to null
        root->right = root->left;
        root->left = nullptr;
        
        // Traverse to the end of the new right subtree
        TreeNode* current = root;
        while (current->right) {
            current = current->right;
        }
        
        // Attach the original right subtree
        current->right = tempRight;
    }
};

Complexity Analysis

The time complexity of this approach is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once. The space complexity is O(1) as we are modifying the tree in place without using any extra space.

Edge Cases

Consider the following edge cases:

An empty tree (root is null) - The output should be an empty list.
A tree with a single node - The output should be the same single node.

Testing

To test the solution comprehensively, consider the following test cases:

Simple trees with varying structures (e.g., left-skewed, right-skewed, balanced).
Edge cases such as an empty tree and a single-node tree.

Thinking and Problem-Solving Tips

When approaching such problems, it is essential to understand the traversal order and how to manipulate pointers effectively. Practice similar problems to develop a deeper understanding of tree manipulations and recursive algorithms.

Conclusion

Flattening a binary tree into a linked list is a common problem that tests your understanding of tree traversals and pointer manipulations. By practicing and understanding the underlying concepts, you can efficiently solve similar problems.

Flatten Binary Tree in C++ (Time Complexity: O(n))